PROPOSITIO XXXI.
Proposita ellipsi possibile est ducere duas aequidistantes ipsam tangentes ad datum intervallum, oportet autem ut datum intervallum neque maius sit maiore axium ellipsis, neque minus minore.
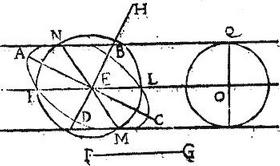
Esto proposita ellipsis ABCD, cuius axes AC. BD, centrum E, datum spatium FG. Aio, quod possibile est ducere duas aequidistantes utrinque ABCD ellipsim tangentes; ita ut ductaram intervallum capiat circulum diametro FG descriptum. Oportet autem ut FG intervallum neque excedat axem ellipsis maiorem AC, neque deficiat ab axe minori DB. Secus enim esset impossibile. Itaque si FG intervallum sit aequale axi maiori AC, vel minori DB; tunc lineae ductae per ipsius axis extrema ad rectos ipsi axi tangent ellipsim apud eamdem extrema; quando quidem ordinatae sunt ad ipsum axem; sed quae tangunt apud extrema maioris axis, in maximo, quae vero apud extrema axis minoris, in minimo distant intervallo, quam esse possent quaelibet eamdem ellipsim tangentes. Si autem FG intervallum minus sit quidem ipso AC axe, maius autem ipso DB. Tunc sicut est diameter FG ad diametrum AC, sic sit diameter BD ad lineam DH. Et quoniam ratio circuli FG ad ellipsim ABCD componitur ex rationibus diametrorum ad diametros, per 8, praemissi: ideo erit circulus FG ad ellipsim ABCD sicut FG ad DH describatur peripheria circuli super ellipsis centrum E ad spatium dimidiae DH; quod spatium cum sit maius, quam ED, minus vero quam EA, descripta peripheria secabit peripheriam ellipsis in aliquo puncto inter A, D; ut puta in punctum K. Ducatur ergo KE, et producatur ad L: diameter ergo erit KL aequalis ipsi DH; et idcirco erit circulus FG ad ellipsim ABC, sicut FG, KL ducatur coniungata diametros ipsius KL. Quae scilicet per aequalia secet ipsam KL eiusque aequidistantes singulas in sectione: quae diameter sit MEN, et per puncta M, N ducantur ipsi KL aequidistantes MP, NQ, quae ordinatae cum sint ad diametrum MN: iam per 17. primi conicorum, tangent ellipsim in punctis M, N. Demonstrandum ergo est, quod ipsarum MP, NQ intervallum capit praecise circulum FG; ita quod tangant utrinque ipsum FG circulum. Secus enim circuli FG positi super puncto O medio inter ipsas, MP, NQ aequidistantes; aut cadit eius peripheria intra ipsas MP, NQ non tangens, aut ipsas secabit: itaque de[S:275]scribatur super O centro circulus tangens utrinque lineas aequidistantes in punctis P, Q; ergo circulus FG maior, aut minor erit circulo PQ eritque circulus FG ad ellipsim ABCD per hypothesim, sicut linea FG ad lineam KL per 27 vero huius, ellipsis ABCD ad circulum PQ est sicut linea KL ad lineam PQ. Igitur ex aequali, circulus FG ad circulum PQ erit sicut diameter FG ad diametrum PQ: sit tertia proportionalis ipsis PQ, FG, ipsa PM; eritque quod ex PQ quadratum ad quadratum FG; ed ideo circulus PQ ad circulum FG, sicut linea PQ ad lineam PM. Eamque ergo rationem habet linea PQ ad PM, et ad FG (cum hae duae proportiones eaedem sint unitertiae. Scilicet circuli PQ ad circulum FG:) aequales ergo sunt PM, FG proindeque prima trium proportionalium PQ aequalis quoque erit secundae FG pars, et totum quod est impossibile, omnino igitur intervallum circuli FG non excedet, neque excedetur ab intervallo ipsarum MP, NQ aequidistantium, et ellipsim ABC tangentium; tangetur itaque ab ipsis. Quod erat demonstrandum.
SCHOLIUM.
Hinc licebit, iisdem suppositis ducere duo plana aequidistantia propositam sphaeroidem figuram solidam tangentia ad datum intervallum, quod tamen neque maius sit maiore, neque minus minore axium ellipsis propositam sphaeroidem figuram describentis.
Quae quidem speculationes, ut scitu iocundae, ita omittendae minimae videbantur: itaque ea, quae Archimedes demonstrare neglexerat, demonstravimus, et complurium, quae ille omiserat, demonstrationes adiecimus caetera curiosiores requirent.