PROPOSITIO XIX.

Quod si sphaeroides plano per centrum ad axem obliquo secetur; similiter ipsum figurae dimidium duplum esse probatur coni super eamdem basim, eumdemque axem constituti.

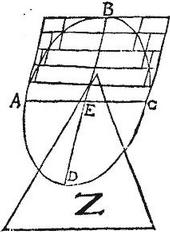
Non alium hic expectes, quam in praemissa, processum ac demonstrationem; hoc excepto quod plana sphaeroides figuram secantia hic obliqua supponuntur ad axem, faciuntque per 26. et 27. praecedentis, solidum secando similes ellipses: quare conus ABC, cylindrus ABC cum caeteris partialibus cylindris habebunt pro basibus ellipses similes. Sunt tamen per 11. et 13. praemissi conorum, et cylindrorum circulares bases habentium segmenta. Cumque per 14. et 15. praecedentis talia coni, et cylindrorum segmenta servent basium proportionem, utpute aequales axes habentia: quare per eadem media, quibus in praemissa, usi sumus, posito cono Z duplo ad conum ABC demonstrabimus portionem ABC nec maiorem, nec minorem esse cono Z; et perinde aequalem.

SCHOLIUM I.

Oportet autem ut BED diameter ellipsis semper incedat per centrum utque AEC, caeteraeque aequidistantes sicut ordinatae ad talem diametrum, ab ea videlicet per medium singulae secandae per 47. primi conicorum elementorum quod et in 9. huius cautum est in formatione figurae tam inscriptae, quam circumscriptae.

SCHOLIUM II.

Notandum etiam, quod sicut in duabus praecedentibus semidiameter EB in quinque partes, et cylindrus ABC in totidem cylindros aequales secatur, sic cum tam semidiameter, quam cylindrus secandus erit in plures partes, utcumque ad demon[S:264]strationem opus fuerit; agendum erit in demonstratione per numerum assumptum: ut scilicet sint cylindri constituentes figuram circumscriptam: cylindri vero componentes figuram inscriptam semper sint unitate pauciores.