PROPOSITIO XVIII.

Dimidium sphaeroidis plano ad axem recto secti, duplum est coni eamdem basim, eumdemque axem habentis.

Esto sphaeroides solidum ABCD, cuius centrum E, de quo abscindatur portio ABC plano per centrum E, et ad axem recto ducto; quae portio per 7. huius erit dimidium sphaeroidis; sitque ABCD ellipsis in solido facta a plano per axem per 16. praemissi; cuius plani cum plano ad axem recto communis: sectio sit AC; quae diameter est circuli in solido facti per 17. praemissi: dico itaque, quo portio ABC (quae di[S:262]midium est solidi) dupla est coni super circulum AC, et axem BE constituti.

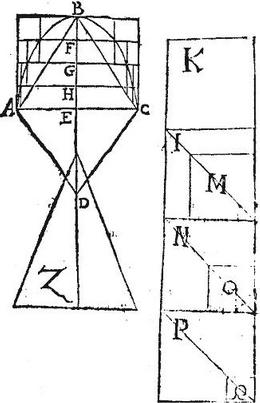
Ponatur cum cono ABC eamdem basim eumdemque axim habens cylindrus ABC; qui per 15. praemissi, triplus est ad conum; ponatur et conus Z duplus coni ABC. Itaque demonstrandum erit, quod portio sphaeroidis ABC aequalis erit cono Z; erit enim conus Z duae tertiae cylindri ABC: si ergo portio ABC aequalis non erit cono Z; sit primum eo maior aliquo excessu; sectaque BE in partes aequales in punctis F, G, H, divisoque cylindro ABC in totidem cylindros aequales per 8. huius, et nonae corollarium fiat figura inscripta portioni; itaut portio addat super figuram inscriptam minus dicto excessu: eritque maior figura inscripta, quam conus Z: post haec exponantur in longum continuatae lineae tot, quot sunt partes ipsius BE, et singulae ipsi BE aequales, super quas constituantur quadrata singula K, IM, NO, PQ; a quibus, primo excepto, auferantur quadrata per ordinem M, O, Q, quae fiunt per ordinem a lineis EF, EG, EH; divisis videlicet singulis quadratorum magnorum lateribus in partes aequales magnitudine, et numero partibus ipsis lineae BE. Unde fiet per 4. secundi Euclidis ut gnomones relicti I, N, P sint per ordinem aequales rectangulis BFD, BGD, BHD singuli singulis: utque quadratum K sit ipsum rectangulum BED. Verum per 21. primi conicorum Elementorum dicta rectangula BED, BFD, BGD, BHD, sunt proportionalia quadratis linearum AE, caeterarumque a punctis F, G, H, ad peripheriam ellipsis ordinatarum quadrata vero proportionalia circulis, quorum ordinatae sunt semidiametri; circuli vero quoniam bases sunt cylindrorum aequos axes habentium proportionales cylindris: igitur, et cilindri quatuor ut ipsae, cuius basis semidiameter est AE; et caeteri, quorum basium semidiametri sunt caeterae tres ordinatae sunt proportionales quadrato K, et tribus gnominibus I, N, P, unde sequitur ex 2. praemissi, ut quadruplum cylindri AHC hoc est totalis cylindrus ABC ad aggregatum trium cylindrorum componentium figuram inscriptam portioni ABC, sit sicut quadruplum quadrati K ad aggregatum trium gnomonum I, N. P: sed per 8. libelli de spiralibus aggregatum quadratorum K, M, O, Q, est plusquam tertia pars quadrupli quadrati K; atque ideo relictum de quadruplo hoc est aggregatum gnomonum I, N, P minus quam duae tertiae dicti quadrupli. Igitur, et figura inscripta portioni minor erit quam duae tertiae cylindri ABC; et perinde minor cono Z: fuerat vero maior, quod est absurdum. Non est ergo maior portio ABC cono Z. [S:263]

Sit autem post haec minor: et tunc per eadem, quae prius fiat figura circumscripta portioni ABC; itaut figura minus excedat portionem, quam conum Z: et proinde conus Z sit maior, quam figura circumscripta. Tunc autem rursus per eadem sequetur ut quadruplum cylindri AHC, hoc est totus cylindrus ABC ad aggregatum quatuor cylindrorum componentium figuram circumscriptam sit sicut quadruplum quadrati K ad aggregatum ex quadrato K, et tribus gnomonibus I, N, P, sed per 8. libelli de spiralibus aggregatum quadratorum M, O, Q, est minus, quam tertia pars quadrupli quadrati K; atque ideo relictum de quadruplo scilicet K, I, N, P, plus erit, quam duae tertiae dicti quadrupli. Igitur et figura circumscripta portioni plus erit, quam duae tertiae cylindri ABC; et perinde maior cono Z: fuerat vero minor. Quod est absurdum. Non est ergo minor portio ABC cono Z; sed nec maior fuit. Erit ergo aequalis; sicut proponitur demonstrandum.