F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de conoidibus et sphaeroidibus figuris Liber primus 17
<- App. -> <- = ->

PROPOSITIO XVII.

Si solidum conoides, quodcumque sit ex tribus praedictis, plano secetur super axem erecto; sectio circulus erit centrum habens in axe.

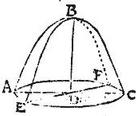
figura 15

Esto solidum, conoides, quodlibet ex tribus memoratis ABC, cuius axis BD, quod secetur plano AEC, cui perpendicularis sit BD, sitque facta sectio AEC. Aio quod AEC sectio circulus est. Nam cum solidum ABC describatur per definitionem, a figura ABC super axem BD fixum circumlata; iam in tali revolutione, linea DC termino D stante, circumferetur, mensurabitque lineas omnes a puncto D in plano secan[S:238]te ad superficiem usque solidi eductas: omnes ergo lineae a puncto D in plano dicto ad peripheriam AEC deductae, ut puta DA, DE aequales erunt ipsi DC: itaque per definitionem, figura AEC circulus erit.

Inizio della pagina
 ->