PROPOSITIO XI.

Quod si excitata sit super diametrum minorem perpendicularis; idem possibile esse demonstrabitur.

Rursum ellipsis esto, cuius diameter maior AB; minor autem DFE: linea FC, perpendicularis ad DFE, non autem ad AB. Aio rursum quod conus aliquis est habens verticem C, atque suscipiens in superficie conica ellipsim ADBE. Producantur, fiantque aequales lineae CAG, CB; et coniuncta BG sit ei perpendicularis CH et erecta super planum GKB, cui plano occurrant productae CDL, CEK, CFM, (constitutae iam in uno plano) et coniungantur puncta L, M, K, quae sunt in una recta; et sicut est rectangulum BMG ad rectangulum BHG sic sit quadratum MK ad quadratum HN, cui aequalis annectatur HO: et circa diametros BG, NHO deducatur circulus quidem, si ipsae BG, NHO sint aequales: ellipsis vero si inaequales: qui circulus sive ellipsis omnino ibit per puncta K, L propter dictam rectangulorum proportionem. Itemque si circulus sit GKB ecce iam conus, cuius basis circulus GKB vertex vero punctum [S:235] C, qui suscipit ellipsim propositam ADBE; quandoquidem extrema diametrorum AB, DE sunt in superficie conica talis coni.

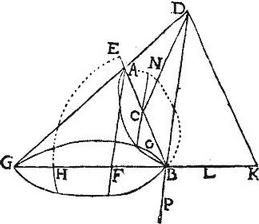
Si autem GKB sit ellipsis; tunc cum HC sit ex centro, et super diametrum maiorem perpendiculariter excitata; iam per praecedentem, conus aliquis erit suscipiens in superficie conica ellipsim GKB: et is igitur conus suscipiet ellipsim propositam ADBE; quoniam videlicet, et in eius coni superficie consistunt extrema diametrorum AB, DE. Et hoc ipsum possibile iam fore proposuimus.