Complexity of 3-manifolds:
When you want to understand some objects, like knots or 3-manifolds, it is natural to define a reasonable complexity and then to try to tabulate them starting with complexity 0, 1, 2, 3, etc. A natural complexity for knots is the crossing number, and knots have been tabulated by many mathematicians, starting from the XIX century. A natural complexity for 3-manifolds is the minimum number of tetrahedra in a triangulation. However, it turns out that using spines instead of triangulations, as it was done brilliantly by Matveev around 1990, we get a much better behaved complexity:
- We get zero on the 3-sphere and on the 3-ball (similarly, the unknot has crossing number zero);
- Complexity is additive on connected sums, while additivity of crossing number for knots is still only a conjecture (true up to a multiplicative constant by a theorem of Lackenby);
- Complexity does not increase when you cut along incompressible surfaces.
- Closed orientable 3-manifolds up to complexity 9 [2] and 10 [12], with Petronio;
- Closed non-orientable 3-manifolds up to complexity 6 [5] and 7 [9], with Amendola;
- Compact hyperbolic manifolds with geodesic boundary and possibly some cusps up to complexity 4 [7], with Frigerio and Petronio;
- Hyperbolic graphs in 3-manifolds up to complexity 5 [16], with Heard, Hodgson, and Petronio.
- Cusped hyperbolic 3-manifolds up to complexity 7, from the SnapPea census by Callahan, Hildebrand, and Weeks;
- Closed 3-manifolds of complexity up to 11, from Burton's Regina;
- Closed orientable 3-manifolds of complexity up to 12, from Matveev's atlas of 3-manifolds.
- A conjectural formula for the complexity of all Seifert manifolds [8], with Petronio;
- A survey on the complexity of 3-manifolds [12];
- A study of the stable complexity, i.e. the complexity stabilized under finite covers [20], with Francaviglia and Frigerio.
- Those having an ideal triangulation with only one edge [4], with Frigerio and Petronio;
- Some hyperbolic knots in handlebodies with six exceptional Dehn surgeries, three of which are handlebodies [6], with Frigerio and Petronio;
- Pick any triangulation and replace every tetrahedron with an ideal regular hyperbolic octahedron [14], with Costantino, Frigerio, and Petronio;
Complexity of 4-manifolds:
I have tried to study smooth closed 4-manifolds experimentally in the same way as it has been done in dimension 3, trying to mimic Matveev's clever use of spines. Of course the setting is much more complicated, and it is hard to obtain useful and meaningful results. I have studied essentially two approaches:
- Use 3-dimensional spines [17];
- Use 2-dimensional polyhedra (called shadows by Turaev) [18], and [35] with Koda and Naoe.
Dehn surgery:
A Dehn filling on a cusped hyperbolic 3-manifold is exceptional when the resulting 3-manifold is not hyperbolic. There are usually infinitely many exceptional fillings on a 3-manifold with multiple cusps, but it is possible to describe all of them with a finite amount of data. Consider for instance the following links
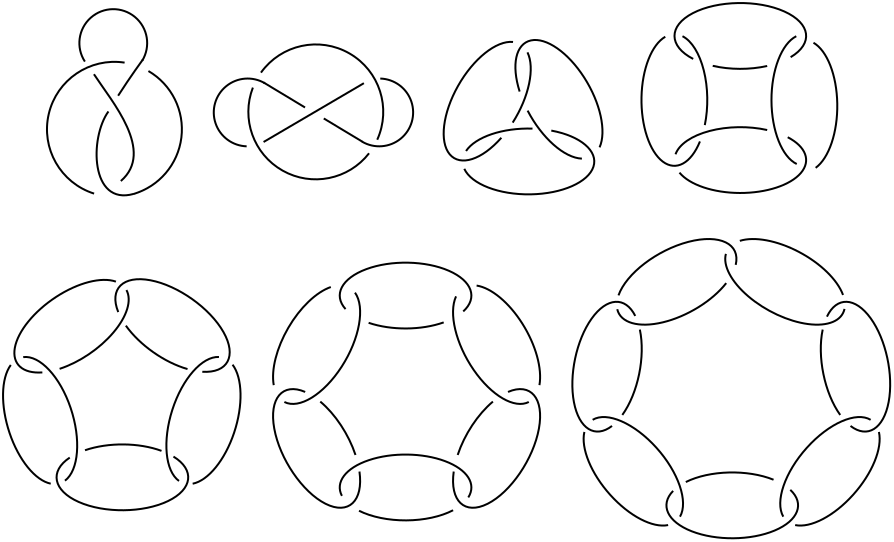
The python code is available on this page and can be used on any link. See the detailed instructions there.
Normal surfaces:
Normal and (octagonal) almost normal surfaces generalize to k-normal surfaces, belonging the cases k=0 and 1 respectively. With Evgeny Fominykh we gave a short proof that a minimal triangulation of an irreducible 3-manifold does not contain any k-normal sphere (with few exceptions) in [15].
Kirby moves:
The short paper [19] answers a nice question on Mathoverflow about Kirby calculus. I show that there is a finite collection of local moves that connected any two surgery presentations of the same 3-manifold via framed links in the three-sphere.
Quantum invariants:
I have tried in the past to use quantum invariants to deduce some interesting topological information on surfaces and 3-manifolds.
In [23] with Costantino we use quantum invariants to construct an analytic family of representations of the mapping class group defined on the unit disc, that includes the finite representations at the roots of unity.
In [25] with Carrega we study the relation between quantum invariants, shadows, and ribbon surfaces. We have extended a theorem of Eisermann that connects quantum invariant and ribbon surfaces in the 3-sphere.
Hyperbolic 4-manifolds:
Various hyperbolic manifolds can be constructed by assembling hyperbolic regular polytopes. In [21] with Kolpakov we use the ideal hyperbolic 24-cell to build hyperbolic four-manifolds with an arbitrary number of cusps, and in [24] with Kolpakov and Tschantz we use the 120-cell to build some hyperbolic four-manifolds with connected geodesic boundary of controlled volume.
The paper [29] is a survey on hyperbolic four-manifolds.
In [30] with Riolo we define a deformation relating two non-commensurable hyperbolic four-manifolds through cone manifolds with cone singularity an immersed surface. This family may be interpreted as a hyperbolic Dehn filling in dimension four.
In [31] with Riolo and Slavich we construct a compact oriented hyperbolic 4-manifold M with odd intersection form. This leads to the first examples of compact oriented hyperbolic n-manifolds without spin structures, for every n ≥ 4. In [33] we extend these techniques to prove that every plumbing of disc bundles over surfaces whose genera satisfy a simple inequality has a convex hyperbolic structure and is contained in some closed hyperbolic 4-manifold.
In [34] with Battista we construct a finite-volume hyperbolic 4-manifold with a perfect circle-valued Morse function. This is the closest possible analouge of a fibration in even dimension.
In [41] I exhibit and study a link of 5 tori in the 4-sphere that has many similarities with the familiar Borromean rings in the 3-sphere.
In [42] with Lin we prove that the Seiberg - Witten invariants of the Davis hyperbolic 4-manifold vanish. To do so we need to study the adjunction inequalities corresponding to 864 genus two totally geodesic surfaces.
Hyperbolic n-manifolds:
Hyperbolic manifolds of arbitrary dimension n form a wide and mostly unexplored area of geometry.
In [36] with Italiano and Migliorini we construct some algebraic fibrations on some manifolds in dimension 5, 6, 7, 8. In dimension 7 and 8, these are covered by some hyperbolic manifolds with finitely presented fundamental group and infinitely many cusps of maximal rank.
In [37] we then refine the 5-dimensional example to build a fibering hyperbolic 5-manifold. These is the first fibering hyperbolic manifold known in dimension higher than 3.
In [43] I describe the monodromy of one fibering hyperbolic 5-manifold as a pseudo-Anosov homeomorphism of the 4-dimensional fiber, in a way that is suprisingly similar to the Nielsen - Thurston theory.
In [39] with Reid we study how spin structures restict to cusp sections. We then use this to certify the existence of Dirac operators with both continuous and discrete spectra in various dimensions.
Tropical geometry:
I have been interested in tropical geometry for some time. In [26] with Golla we study the topological notion of decomposing a 4-manifold into pair-of-pants that arises naturally from this area.
Spines of minimal area:
In [28], with Novaga, Pluda, and Riolo, we raise the question whether every closed riemannian manifold has a spine of minimal area (that is, codimension one Hausdorff measure). We answer it affirmatively in dimension 2 and study the spines of minimal lengths on constant curvature surfaces. We introduce the spine systole, a proper function on moduli spaces.
Geometric group theory:
Hyperbolic geometry is of course tightly connected with geometric group theory. In [37] with Italiano and Migliorini we use a fibering hyperbolic 5-manifold to build the first example of a finite type subgroup of a hyperbolic group that is not hyperbolic.
In [43] I further prove that this subgroup can be made CAT(0). Therefore there is a locally CAT(0) space whose fundamental group is not hyperbolic, and does not contain Z+Z.
In [38], together with Llosa Isenrich and Py, we construct a hyperbolic group that contains a subgroup that is F3 and not F4. This is related to [36].
Coxeter polyhedra:
Many of the higher-dimensional hyperbolic manifolds that I have studied were constructed starting from some specific Coxeter polyhedron. The paper [44] is a survery on these beautiful objects.

