PROPOSITIO XXX

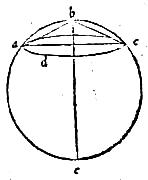
212 Si a polo alicuius circuli in sphaera signati recta linea ad sphaerae superficiem ducatur, quae sit aequalis lineae ab eodem polo super circuli ipsius periferiam descendenti, necesse est eam in eiusdem circuli periferiam terminari.

213 A polo a circuli bcd in sphaera signati ducatur ad eius periferiam recta ac, cui aequalis ae ab eodem polo a ducatur ad superficiem sphaerae: aio quod e terminus est in ipsa periferia bcd. 214 Intelligatur enim planum per rectam ae et per centrum sphaerae eritque eius plani et sphaerae communis sectio, per primam, circulus bad, maior per 6, qui secet circulum bcd in punctis bd. 215 Itaque, si punctum e fuerit alterum punctorum bd, tunc constat propositum. 216 Secus autem iungam rectam ab, eritque per diffinitionem poli ab recta aequalis ipsi ac. 217 Sed <ac> fuit aequalis <ipsi> ae; igitur ab linea aequalis erit ipsi ae. 218 Quare arcus ab ae sunt aequales, pars et totum, quod est impossibile. 219 Punctum igitur e non alio cadet quam in periferiam bcd. Quod volumus demonstrandum.