PROPOSITIO XXXI

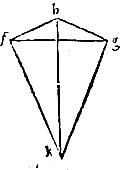
220 Quibuscunque duobus punctis in sphaerae superficie datis, circulum maiorem qui per ea transeat designare.

221 Data puncta in superficie sphaerae sunt a b: oportet describere circulum maiorem qui per ab puncta incedat. 222 Si duo puncta a b sunt per diametrum opposita, infiniti circuli maiores describi poterunt transeuntes per ea: omne enim planum ductum per lineam rectam [S:5r] quae puncta data connectit, quae tunc diameter est sphaerae, faciet per primam et 6 huius circulum maiorem. 223 Si autem puncta data non sint in diametro, tunc, per 29 praemissam, capiatur sphaerae diametros et latus quadrati descripti intra circulum cuius est illa diameter, hoc est intra circulum maiorem ipsius sphaerae, et ad dicti lateris quadrati spacium super polo quidem a circulus cd, super polo autem b circulus ce describatur. Eruntque <per> 27 huius cd ce circuli maiores; quare secabunt se per aequalia. 224 Alteram igitur sectionum c coniungam cum punctis ab per duas rectas ac cb singulas, videlicet lateri dicti quadrati aequales. 225 Mox super c polo ad spacium unius earum, ut puta ac, describam circulum, qui per praecedentem ibit per b terminum alterius eritque, per 27 huius, circulus maior. Quod faciendum proponebatur.