22

39 Cubus triplus est ad pyramidem in eadem sphaera descriptam.

Nam, per 18^am huius, ratio sesquitertia, hoc est 36 ad 27 dupla est eius, quam habet cubus ad octahedrum. Item, per undecimam huius, ratio 27 ad 4 dupla est eius, quam habet octahedrum ad pyramidem. 40 Ergo, per aequam proportionem, ratio 36 ad 4 dupla est eius, quam habet cubus ad pyramidem. Sed haec eadem ratio 36 ad 4 per 11^am Octavi, dupla est eius, quam habet 6 ad 2. Ergo cubus ad pyramidem, sicut 6 ad 2 hoc est sicut 3 ad 1 videlicet triplus. Sicut proponitur demonstrandum.

41 Id idem potest aliter ostendi. Erecta enim pyramide super basim cubi ad altitudinem cubi, haec pyramis quadrata erit aequalis tetrahedro. Sed cubus ad hanc pyramidem triplus per 7^am Undecimi. Ergo idem [S:130] cubus ad tetrahedrum triplus. Quod autem pyramis ipsa cubi aequalis sit tetrahedro, patet. Quoniam per 20^am huius, sesquitertia ratio dupla est eius, quam habet basis cubicae pyramidis ad basim tetrahedri. 42 Rursum sesquitertia ratio dupla est eius, quam habet fastigium tetrahedri ad fastigium cubicae pyramidis, per 2^um corollarium 18^ae praemissi libelli. Ergo bases cubicae pyramidis, et tetrahedri reciprocae sunt celsitudinibus. Quare per 9^am Undecimi, cubica pyramis tetrahedro aequalis est. Quod supererat demonstrandum.

Idem sequitur, si pyramidis vel tetrahedri columnam triangulam erigas, quae cum sit tripla tetrahedro et aequalis cubo, rursus arguitur cubus ad tetrahedrum triplus. 43 Quod autem praedicta columna triangula sit aequalis cubo: patet, quoniam bases in ipsis sunt altitudinibus reciprocae per corollarium dictum et per 20^am huius.

Idem aliter et quarto modo demonstrabimus (quae curiositas est ingeniorum) sic. Diameter sphaerae potentialiter tripla est ad latus cubi sibi inscripti, per 18^am praecedentis. Ergo ad eius dimidium (quanta est perpendicularis a centro sphaerae ad basim cubi per 8^am huius) erit duodecupla. Item, per 5^am huius, sphaerae diameter est trigecupla sexcupla ad perpendicularem a centro sphaerae ad basim pyramidis. 44 Igitur perpendicularis cubi, ad perpendicularem pyramidis potentialiter erit tripla. Quoniam vero ex ductu perpendicularis a centro sphaerae ad basim solidi regularis, in totam superficiem solidi producitur, triplum soliditatis: idcirco triplum soliditatis cubi ad triplum soliditatis pyramidis rationem habet compositam ex rationibus duabus, scilicet ex ratione perpendicularium et ex ratione superficierum. Sed perpendicularis cubi ad perpendicularem pyramidis, dudum ostensa fuit potentialiter tripla. 45 Cubica vero superficies ad pyramidis superficiem, per 21^am huius potentialiter quoque tripla est. Igitur ratio tripli soliditatis cubicae ad triplum soliditatis pyramidis, potentialiter sumpta, componetur ex duabus triplis rationibus. Quare potentialiter erit nonupla. Et ideo triplum cubi ad triplum pyramidis erit nonuplum potentialiter. Unde et cubus ad pyramidem item potentialiter nonuplus et perinde in magnitudine triplus. Sicut tribus aliis processibus dudum demonstratum fuit. Et hic est quartus demonstrationis modus.

Repetitio Pro Calculo

46 Et quoniam, ingeniose Lector, harum diametrorum, laterum, perpendicularium ratio et collatio constat per calculum, ideo repetemus hic omnia, quae circa sphaeram, pyramidem, octahedrum et cubum tradita sunt, in lineamento et calculo, ut repetita melius teneantur. Sic. Super diametrum ab centrumque k stet semicirculus [S:131] adb sitque ac dupla ipsius cb et excitatis perpendicularibus cd, ke, kf.

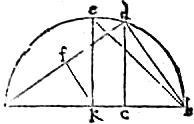
47 Connectantur ad, db, be. Unde constabit ex 16^a7 praemissi, quod posita ab diametro sphaerae, erit ad latus pyramidis in sphaera descripti. Per 17^am eb latus octahedri. Per 18^am bd latus cubi. Per 4^am huius, ac perpendicularis a vertice pyramidis ad basim. Per 5^am huius, kc perpendicularis a centro sphaerae ad basim pyramidis. Per 6^am huius kf perpendicularis a centro sphaerae ad basim octahedri. Nam per 8^am est dimidium ipsius bd. 48 Et per 9^am aequalis perpendicularis a centro sphaerae ad basim cubi. Item ex 16^a praemissi, constat cd esse semidiametrum circuli circumscribentis basim pyramidis. Per 12^am quoque huius, patet triangulum octahedri, et quadratum cubi ab eodem circulo circumscribi. Namque be latus octahedri ad semidiametrum dicti circuli triplum et bd latus cubi ad eandem semidiametrum est potentialiter duplum. Cum illud latus ad hoc sit potentialiter sesquialterum. 49 Exponetur nunc in tabella numerarius calculus, per quem nihilominus omnia demonstrantur.

ab diameter sphaerae supponitur 12 bk semidiameter eius 6 ad latus pyramidis 96 be latus octahedri 72 bd latus cubi 48 ac perpendicularis a vertice pyramidis ad basim 8 cb excessus diameter super dictam perpendicularem 4 kc perpendicularis a centro sphaerae ad basim pyramidis 2 kf perpendicularis a centro sphaerae ad basim octahedri et etiam ad basim cubi 12 cd semidiameter circuli circumscribentis basim pyramidis 32 Semidiameter circuli circumscribentis quadratum cubi et triangulum octahedri 24

Ad quam videlicet latus octahedri (quod et trianguli) triplum: latus vero cubi (quod et quadrati) duplum est.

Quae quidem pertinent ad tria solida, scilicet pyramidem, octahedrum et cubum.

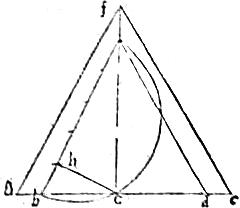
50 Et ne quid intentatum relinquatur, subiungemus nunc duorum, quae restant, solidorum lineamentum et calculum. Ponatur ab semidiameter sphaerae, super quam describatur semicirculus bca. Et in diametro, sit ah quadrupla residui bh. Et excitata hc perpendiculari, coniungatur bc, ca et producantur utrinque. Sitque ipsi ab aequalis bd atque connectatur ad quae, per 21^am [S:132] praemissi, erit latus icosahedri in sphaera, cuius semidiameter ab. 51 Et quoniam ah quadrupla est ipsius hb. Ideo quadratum ipsius ac quadruplum erit quadrati bc et ac dupla ipsius bc et bd aequalis ipsi ab. Iam, per 11^am Secundi, quod fit ex ac in ipsam cb aequum est quadrato ipsius cd atque ideo per 16^am Sexti si ac secetur secundum extremam et mediam rationem; maior eius portio erit cd. Vel quoniam ab ad ipsam bc potentialiter quincupla est, ideo ac (quae dupla est ipsius bc) divisa secundum extremam et mediam rationem, maior eius portio erit cd per 2^am praemissi libri. 52 Producatur ca et ponatur cf latus cubi in dicta sphaera locati. Quod quidem ad semidiametrum potentialiter sesquitertium est ad ipsam vero ac sicut 5 ad 3 et agantur ef, fg ipsis da, ab aequidistantes. Unde ex similitudine triangulorum sequetur proportio linearum.

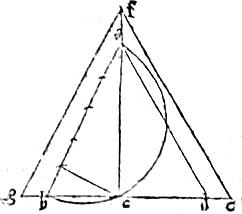
Atque per 7^am praemissi, sicut ipsius ac secundum extremam et mediam rationem divisae maior portio est cd ita et ipsius cf similiter sectae maior pars erit ce. Cumque cf sit latus cubi, iam per 20^am praemissi, ce fiet latus dodecahedri in eadem sphaera clausi.

53 Si autem ponatur ac semidiameter circuli vel latus hexagoni, tunc, quoniam ac per mediam et extremam rationem sectae maior portio est cd. Ideo per 12^am praemissi cd erit latus decagoni a tali circulo circumscripti, et per 13^am ad latus pentagoni.

Et quoniam ac ad ipsam ab semidiametrum sphaerae potentialiter est sicut 4 ad 5. Et ipsius ac dicto modo divisae maior portio est cd. Ideo sequitur hoc corollarium, quod ipsum ad latus icosahedri potest ipsas ac, cd.

54 Item, quoniam ab semidiameter sphaerae potentialiter quincupla est ad ipsam bc quod est dimidium ipsius ac ideo diameter sphaerae potentialiter etiam quincupla est ad totam ac quae est semidiameter circuli circumscribentis pentagonum, cuius latus est ipsum ad latus icosahedri in tali sphaera locati. Quod autem linea ad sit latus pentagoni in dicto circulo positi, patet per 13^am praemissi, quoniam potest ipsa ac, cd latera hexagoni et decagoni a tali circulo clausularum. Et habes secundum hoc corollarium.

55 Constat etiam quod sphaerae semidiameter aequalis est dimidio lateris hexagoni et lateri decagoni in circulo praedicto descriptorum pariter acceptis. Namque ab sphaerae semidiameter aequalis fuit ipsi bd [S:133] quae componitur ex bc dicto dimidio, et ex cd latere decagoni. Et hoc est tertium corollarium.

56 Notandum etiam quod haec eadem corollaria sequebantur in descriptione et lineamento 19 praecedentis libri.

Si sphaera circumscribat dodecahedrum et cubum: tunc latus cubi est linea, quae subtendit angulum in pentagono dodecahedri. Et hoc etiam corollarium constat in 20^a praemissi.

Nunc veniamus ad praxim calculi theoriam comprobantes et sphaerae semidiametrum partium 6 sicut antea, ponentes.

ab semidiameter sphaerae 6 ah 44/5 hb 11/5 ch 22/5 ac 284/5 bc 71/5 ad latus icosahedri, scilicet V 72 minus 10364/5 cf latus cubi 48 cg 12 ce latus dodecahedri 60 minus 12

Quae singula respondent iis, quae superius demonstrantur.

57 Hactenus quae circa latera et bases ac perpendiculares pyramidis, octahedri, atque cubi et eorum collationes. Nec non circa latera icosahedri atque dodecahedri consyderanda sunt, tradidimus. Deinceps ad perpendiculares, bases, superficies ac soliditates horum duorum, et collationem demonstrandam veniemus. Et hinc secundum hunc libellum terminabimus.