PROPOSITIONES
1a Si in coni sectione vel circuli periferia relictum sit quoddam14 punctum extra: et ab ipso in sectionem excitentur duae lineae: quarum una quidem tangat, altera vero secet ad duo puncta; et quam habet rationem tota secans ad extra receptam inter punctum et sectionem, hanc habeant segmenta15 intus receptae ad idem punctum continuata: tunc a tactu ad punctum dividens ducta linea coincidit sectioni, et ab occursu ad extra relictum punctum acta linea tangit sectionem.
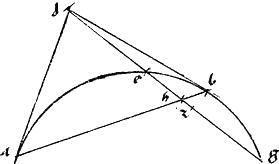
[S:130] Sit enim coni sectio, vel circuli periferia abg. // Relictum [A:99v] extra punctum d. // Tangens sectionem db. // Tactus b. // Secans sectionem deg apud puncta e g. // Et sicut est gd ![]() de, sic sit gz
de, sic sit gz ![]() ze.
ze.
// Dico iam quod linea bz producta coincidit sectioni: et ducta ab occursu ad punctum d tangit sectionem.
// Cum enim dg secet sectionem ad duo puncta, non erit iam diameter ipsius: potest igitur quis per d diametrum ducere, quare et tangentem. // Ducatur tangens da. // Et coniuncta ba secet ipsam eg si possibile est non apud z sed apud h. // Quoniam16 igitur tangunt ad db coniungit autem tactus ab. // Secat autem periferiam deg apud e g ipsamque ab apud h. Iam per 37am tertii Conicorum, erit ut gd ![]() de, sic gh
de, sic gh ![]() he. // Supponitur autem ut gd
he. // Supponitur autem ut gd ![]() de, sic gz17
de, sic gz17 ![]() ze. // Igitur sicut gz
ze. // Igitur sicut gz ![]() ze sic gh
ze sic gh ![]() he. // Et coniunctim, sicut ge
he. // Et coniunctim, sicut ge ![]() eh sic ge
eh sic ge ![]() ez. // Ergo per 9am quinti Euclidis he ez aequales: quod est absurdum. // Quare ab non alibi, quam apud z secat eg lineam tangit autem ad apud a. // Igitur verum est, quod proponitur demonstrandum.
ez. // Ergo per 9am quinti Euclidis he ez aequales: quod est absurdum. // Quare ab non alibi, quam apud z secat eg lineam tangit autem ad apud a. // Igitur verum est, quod proponitur demonstrandum.
// SCHOLIUM
Verum quo ad hyperbolen, attendendum quod necesse est punctum d constituit intra contentum sub non tangentibus18 angulum: nam in hyperbole non est possibile aliunde duci utrinque tangentes ad sectionem: quemadmodum in fine secundi abunde fuit traditum.