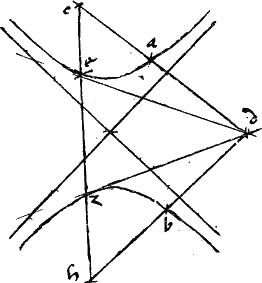
[A:105v] 18^a Sint rursus contrapositae a b et punctum d intra extrinsecum angulum non tangentium⁹⁷ et ducatur dbh secans sectionem b ad unum solum punctum b uni non tangentium⁹⁸ aequidistans. Et dac⁹⁹ secet sectionem a similiter apud a punctum dumtaxat. Ponaturque ipsi db aequalis bh nec non ipsi da aequalis ac; tunc ch coniuncta coincidet sectionibus, ut pote apud e z et ipsae ed dz tangent sectiones.

Ducatur enim tangentes de dz. // Et coniuncta ez veniet omnino per puncta c h. // Nam si per c solum veniat, non erit, per 31 tertii Conicorum, ipsi db aequalis bh. // Si autem per h solum, non erit, per eamdem, ipsi da aequalis ac. // Si vero per neutrum, neutra iam erit aequalis alteri: // Quae cum sint contra hypothesim astruitur propositum: ut scilicet cum ez veniat per c h puncta, et vicissim ch per ipsa e z puncta incedat: // tangunt autem periferias ipsae de dz. // Verum ergo quod proponitur.