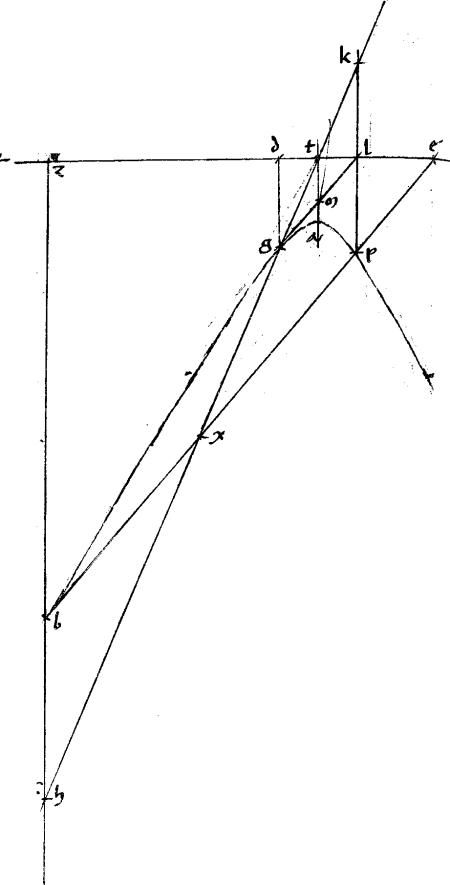
114 [A:75r] [S:100] 21am Iisdem subiectis; si in sectione duo puncta relicta sint: et per ipsa ducantur lineae, altera quidem penes tangentem, altera vero penes tactus coniungentem secantes invecemque et sectiones; erit, ut contentum168 sub iis, quae a concursu tangentium sectionibus coincidunt, ad quadratum, quod fit ex tangente, sic contenta sub ipsarum se invicem secantium portionibus ab incidentia receptis ad periferias sectionum.
115
Sint enim ea, quae prius. // Relicta autem sint169 in sectione ab duo puncta h, c. // Per quae ducantur, penes az tangentem nxhopr, csf170 penes autem ag tactus coniungentem hlm, coq![]()
![]()
![]() . // Per tactum autem a centrumque e linea xame
. // Per tactum autem a centrumque e linea xame![]() t171. // Dico iam quod est ut
t171. // Dico iam quod est ut ![]() 172 bzd
172 bzd ![]()
![]() az sic
az sic ![]() co
co![]()
![]()
![]() noh. //
116
Nam, cum per 47am primi Conicorum nx aequalis sit xh iam per 6am secundi Elementorum
noh. //
116
Nam, cum per 47am primi Conicorum nx aequalis sit xh iam per 6am secundi Elementorum ![]() noh una cum
noh una cum ![]() xh aequale est
xh aequale est ![]() to xo. // Itaque, quoniam propter similitudinem figurarum, ut est
to xo. // Itaque, quoniam propter similitudinem figurarum, ut est ![]() xo
xo ![]()
![]() xo
xo![]() totum scilicet ad totum, sic est
totum scilicet ad totum, sic est ![]() xh
xh ![]()
![]() xhm ablatum ad ablatum: erit, per 19am quinti
xhm ablatum ad ablatum: erit, per 19am quinti ![]() noh
noh ![]()
![]() h
h![]()
![]() m reliquum ad reliquum sicut
m reliquum ad reliquum sicut ![]() xo
xo ![]()
![]() xo
xo![]() totum ad totum.
117
// Et propter similitudinem figurarum, sic
totum ad totum.
117
// Et propter similitudinem figurarum, sic ![]() az
az ![]()
![]() azt et sic
azt et sic ![]() al
al ![]()
![]() alm. // Verum aequale est
alm. // Verum aequale est ![]() azt
azt ![]() lo byz per primam praecedentium additarum. Item aequale est
lo byz per primam praecedentium additarum. Item aequale est ![]() ho
ho![]() m
m ![]() corf sicut mox ostendetur in scholio173. // Igitur sicut
corf sicut mox ostendetur in scholio173. // Igitur sicut ![]() az
az ![]()
![]() byz sic [[... huius]]174
byz sic [[... huius]]174 ![]() noh
noh ![]()
![]() corf.
118
// Et sicut fuit in praemissa conversim
corf.
118
// Et sicut fuit in praemissa conversim ![]() bzr
bzr ![]()
![]() 175 bzd sicut
175 bzd sicut ![]() 176 hlzp
176 hlzp ![]()
![]() hlx. // Ita hic erit et
hlx. // Ita hic erit et ![]() bzy
bzy ![]()
![]() 177 bzd sicut
177 bzd sicut ![]() corf
corf ![]()
![]() co
co![]() . // Quare ex aequali, erit, ut
. // Quare ex aequali, erit, ut ![]() az
az ![]()
![]() 178 bzd sic
178 bzd sic ![]() noh
noh ![]()
![]() co
co![]() . // Et conversim ut
. // Et conversim ut ![]() 179 bzd
179 bzd ![]()
![]() az sic
az sic ![]() co
co![]()
![]()
![]() noh. // Quod erat demonstrandum.
noh. // Quod erat demonstrandum.
Scholium
119
Quod autem ![]() ho
ho![]() m aequum sit
m aequum sit ![]() corf patet sic
corf patet sic ![]() alm aequum est
alm aequum est ![]() hz per corollarium secundae huius: vel per 2am additarum praecedentium. // Commune apponatur
hz per corollarium secundae huius: vel per 2am additarum praecedentium. // Commune apponatur ![]() mlq
mlq![]() et fiet
et fiet ![]() aq
aq![]() aequum
aequum ![]() hz et
hz et ![]() mlq
mlq![]() simul. // Rursus autem per corollarium secundae et ***180
simul. // Rursus autem per corollarium secundae et ***180 ![]() aq
aq![]() aequum est
aequum est ![]() cqzf. //
120
Igitur
cqzf. //
120
Igitur ![]() cqzf aequale
cqzf aequale ![]() hz et
hz et ![]() mlq
mlq ![]() similiter sumptis. // Commune auferatur
similiter sumptis. // Commune auferatur ![]() qzro. // Et supererit
qzro. // Et supererit ![]() ho
ho![]() m aequale
m aequale ![]() corf. Quod demonstrationi praemissae deerat demonstrandum.
corf. Quod demonstrationi praemissae deerat demonstrandum.