2a Iisdem subiectis, si in coni sectione, vel circuli periferia relictum sit quoddam6 punctum: et per ipsum aequidistantes ducantur tangentibus usque ad diametros; factum quadrilaterum ad unam [A:65v] tangentium, unamque diametrum aequale facto triangulo ad eandem tangentem alteramque diametrum.
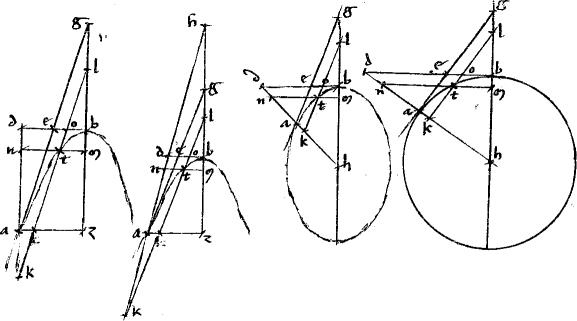
6 [S:87] Sit enim coni sectio vel circuli periferia ab. // Tangentes autem aeg, bed. // Diametri deinde ad bg7 in ellipsi et circulo coincidentes ad centrum h. // Et8 az ordinata ad gbh9 diametrum ut in precedenti. // Et relictum sit quoddam10 punctum t in sectione, per quod ducantur penes ipsas tangentes ipsae ktl mtn. // 7 Dico iam quod aequale est triangulum lbo quadrilatero odnt existente iam o puncto, in quo ktl secat ipsam deb tangentem. // Namque in parabola, per 42am primi Conicorum triangulum lmt aequale est quadrilatero bmnd. In hyperbole11 vero, ellipsi et circulo, ut iam demonstratum12 in processu 47ae eiusdem libri. 8 // Igitur communi ablato quadrilatero bmto supererit triangulum lbo aequale quadrilatero odnt. // Quod est demonstrandum.