[A:65r] [S:86] APOLLONII PERGAEI CONICORUM ELEMENTORUM LIBER TERTIUS

PROPOSITIONES, QUAE SUNT THEOREMATA

1 1^a Si coni sectionem vel circuli periferiam lineae attingant: ducantur autem per tactus diametri coincidentes tangentibus; erunt aequalia secundum summitatem contigua triangula.

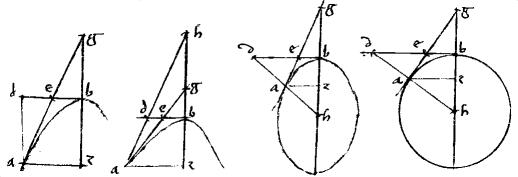
2 Sit coni sectio, vel circuli periferia ab //. Quam tangant ag, bd apud ipsa a, b puncta. Coincidentes ad e. // Et ducantur per a, b diametri sectionis gb, da coincidentes tangentibus ad puncta g, d. 3 // Dico iam quod aequale est triangulum ade triangulo ebg. // Ducatur enim ab a ad ipsam bg diametrum ordinate ipsa az. // Eritque per corollarium 42^ae praecedentis primi¹ in parabola quidem gaz triangulum aequale parallelogrammo dz. // Et ablato communi trapezio aebz. Supererit triangulum ade aequale iam triangulo ebg quod² est propositum. 4 // In hyperbola autem, ellipsi, circuloque coincidant diametri ad centrum h. // Eruntque, per additam post 42^am praemissi libri triangula ahg, dhb invicem aequalia: // Commune auferatur trapezium degh in hyperbola: in ellipsi vero circuloque trapezium aebh et supererunt triangula ade³, ebg aequalia. // Quod proponebatur demonstrandum.

Scholium⁴

5 Lineamenta huius theorematis ex corollario 42^ae praemissi libri primi eiusque additae sumpta sunt⁵ unde et demonstratio.