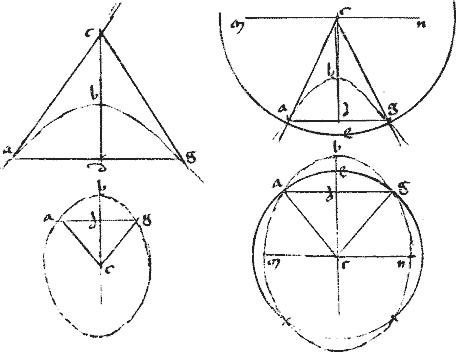
[A:54v] 47a Datae hyperboles, vel ellipseos axim invenire.
Sit hyperbole vel ellipsis abg. // Oportet utique ipsius axim invenire.
// Inveniatur301, et sit cd. // Centrum autem sectionis c. // Igitur cd in se ordinate ductas per medium et ad rectos secat. // Ducatur kathetus gda. // Et coniungantur cd302 cg ca. // Quod igitur303 gd aequalis ipsi da iam per 4am primi Euclidis gc aequalis erit ca. // Cumque g assumptum punctum datum sit: et per 45am huius c centrum datum: dabitur iam gc. // Quare super centro c spatioque cg circulus descriptus ibit per a. // Datisque iam a g punctis: datur ag positione: datur et eius medium punctum d. // Sed c datum. Igitur et dc positione datur.
// Componitur autem sic.
// Sit data hyperbole vel ellipsis abg. // Coniungatur eius centrum c cum relicto in periferia puncto g. // Et super centro c spatioque cg circulus describatur gea304. // Et coniuncta ga bifariam secetur apud d et coniungatur ca cd et producatur cd ad periferiam in b.
// Quoniam itaque gd aequalis da communis autem de305 atque ipsae ac cg per diffinitionem circuli aequales: ideo, per 8am primi Euclidis et anguli aequis oppositi lateribus aequales erunt: igitur anguli adc cdg aequales et perinde recti.
// Itaque cdb per medium et ad rectos secat ipsam adg. // Quare, per diffinitionem axis est cdb. // Qui describendus erat.
// Ducatur et per centrum c mcn306 aequidistans ipsi ag quae307 per diffinitionem mcn axis ipsi cdb axi coniugatus. // Namque horum axis uterque secat alterum eiusque parallelos bifariam, per 15am praemissi, in ellipsi: per 16am vero eiusdem in contrapositis hyperbolis.
// Igitur factum, quod faciendum proponebatur.