45^a Data ellipsi, vel hyperbola, centrum sectionis invenire.

Sit data ellipsis, vel hyperbole bd. // Oportet eius centrum invenire.

[A:54r] // Inveniantur, per praecedentem, duae diametri sectionis, quae sint ab gd quae se invicem secent apud e.

// Quod per diffinitionem centrum erit sectionis.

// Quod erat faciendum.

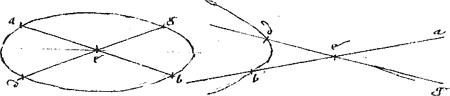
Notandum quod non proponit Apollonius paraboles centrum invenire. Nam cum paraboles diametri sint aequidistantes; quemadmodum in 46^a praecedentis, demonstratum est²⁹⁴. // Parabola iam centrum non habet, diametris non coincidentibus.

// Porro centri circuli inventionem docuit Euclides in tertio Elementorum libro.