27^a Si ellipsim, vel circuli periferiam duae linae tangant, si quidem coniungens tactus²¹² per centrum erit²¹³; aequidistantes erunt tangentes. Si autem non; coincident ad easdem partes centri.

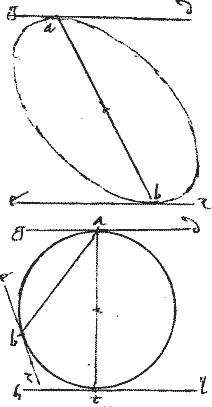
Sit ellipsis vel circulus ab. // Quae ad puncta a b tangant ipsae gd ez. // Et coniuncta ab transeat prius per centrum.

// Dico tunc quod aequidistat²¹⁴ ipsae gd²¹⁵ ez. // Nam, cum diameter sit ab tangens autem dg iam²¹⁶ , per 47^am praecedentis, ab diameter bifariam secabit ordinate ductas ipsi gd aequidistantes. // Sed per 6^am huius, ipsis bifariam sectis aequidistabit ez. // Igitur et ipsa ez aequidistat ipsi gd²¹⁷

// Quod est propositum.

// Vel quoniam per [[additam]]²¹⁸ 32^ae praemissi, tam gd quam ez ordinate ducta est ad ipsam ab diametrum. Et perinde aequidistat²¹⁹.

// Vel quoniam gd ez per conversionem 47^ae praecedentis libri, sive per 6^am huius, aequidistat²²⁰ ordinate applicatis et perinde per medium sectis ad²²¹ ab diametrum²²². Et ideo sunt inter se aequidistantes.

// Sed non sit ab per centrum, ut in 2^a descriptione: Et ducatur diameter at.

// Et per t linea htl tangens: eritque, sicut dudum demonstravimus hl aequidistans ipsi gd. // Igitur ez producta coincidet ipsi dg ad easdem partes centri, in quibus est ab. // Sicut fuit demonstrandum.