17^am Contrapositarum ad coniunctionem, communes sunt non tangentes¹⁴⁴.

Sint coniunctae contrapositae: quarum diametri coniugatae ab gd centrum autem e.

// Dico quod communes sunt ipsarum non tangentes¹⁴⁵.

// Ducatur enim tangentes sectiones apud quatuor puncta a b g d quae sint zah hdt tbm¹⁴⁶ cgz.

// Eritque zhtc parallelo[A:45v]grammum. Coniungantur igitur zet ceh lineae, quae quidem erunt iam diametri parallelogrammi singulae bifariam sectae apud e punctum. // Et diametri sectionum videlicet ab gd sunt, per 34^am primi lateribus parallelogrammi sibi parallelis aequales.

// Itaque, cum per ultimam praecedentis libri, ipsa ab et perinde tam cz quam th possit speciem adiacentem ad dg itemque, cum per eandem, ipsa dg et perinde tam ct quam hz possit speciem adiacentem ad ab iam et harum dimidiae poterunt quadrantem singulae talium specierum. Hoc est ipsarum cg gz td dh unaquaeque poterit quadrantem speciei ad dg adiacentis: et ideo, per primam huius, ipsae zet ceh non tangentes¹⁴⁷ erunt tam hyperboles g quam hyperboles d item ipsarum ha az cb bt singulae poterunt quadrantem speciei ad ab positae: et ideo rursum per primam huius, ipsae eae dem zet ceh non tangentes¹⁴⁸ erunt tam sectionis a quam sectionis b. // Quod erat demonstrandum.

[S:61]

SCHOLIUM

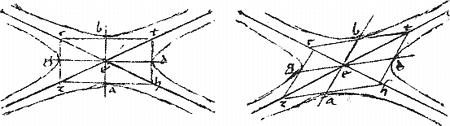
Notandum autem quod ex his quatuor contingentibus contrapositas ad coniunctionem, ductis primum binis ad non tangentes¹⁴⁹: reliquae duae ad harum extrema coincidunt. Utpote ductis cbt haz sectiones apud a b puncta tangentibus, reliquae duae, quae reliquas duas sectiones apud g d puncta tangunt, coincident ipsis cbt haz apud ipsa c t h z puncta. // Namque, cum ex prima huius, ipsa cgz tangens possit totam speciem, quae ad gd et per ultimam praemissi aeb diameter possit eandem speciem: iam aequalis erit cgz ipsi aeb et similiter eidem aeb aequalis erit hdt. // Itemque ipsi ged aequales erunt ipsae tbc haz et harum dimidiae illarum dimidiis. // Quo fit ut tangentes tangentibus coincidant ad quatuor puncta non tangentium¹⁵⁰ in angulis parallelogrammi propter aequidistantiam diametrorum et tangentium¹⁵¹

Manifestum est ergo quod quatuor lineae tangentes contrapositas ad coniunctionem apud extrema coniugatarum diametrorum ad quatuor puncta non tangentium concurrunt, faciuntque parallelogrammum sive rectangulum sive non rectangulum iuxta ductum diametrorum, [A:46r] cuius centrum est ipsum sectionum centrum, ac diagonales lineae ipsae non tangentes¹⁵².

Namque talium quatuor linearum tangentium, binae oppositae sunt aequidistantes per additam 32^ae praemissi: vel per additam post 43^am praemissi et per ultimam praemissi et primam huius, sunt aequales diametro, cui aequidistat.

Item manifestus est, quod contrapositas ad coniunctionem in infinitum productae sicut communibus non tangentibus¹⁵³, ita et sibi invicem approximantes, numquam tamen coincidunt.