[S:57] 10a Si linea quaedam secans81 hyperbolen coincidat utrique82 non tangentium83; contentum rectangulum sub receptis lineis inter non tangentes84 et sectionem aequale est quadranti factae speciei ad diametrum, quae secantem lineam, eiusque parallelos bifariam secat.
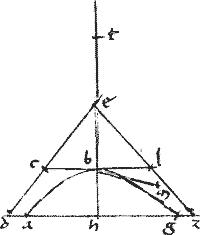
Sit hyperbole abg. // Non tangentes de ez. // Linea dz secans sectionem apud a g et non tangentes apud d z quae bifariam secetur apud h cumque da gz per 8am praecedentem sint aequales; erit et ag bifariam secta apud h. // Et coniungatur he et ponatur ipsi be aequale et. // Eritque bt diameter per corollarium 47ae praemissi. // Et ipsi tb ad rectos bm ita ut, sicut est ![]() thb
thb ![]()
![]() ah sic sit tb
ah sic sit tb ![]() bm unde, cum bt sit diameter, erit per conversionem 21ae primi, bm rectum speciei latus.
bm unde, cum bt sit diameter, erit per conversionem 21ae primi, bm rectum speciei latus.
// Dico iam quod ![]() daz vel
daz vel ![]() dgz est quarta pars
dgz est quarta pars ![]() tbm.
tbm.
// Ducatur enim cbl tangens sectionem apud b quae per 5am huius aequidistabit ipsi dz quandoquidem ipsae ah hg aequales85.
// Itaque quoniam dz bifariam secta est apud h ideo, per 5am secundi Euclidis
|
Item quoniam bt bifariam secta est apud e ideo per 6am eiusdem
|
Et quoniam per primam sexti Euclidis sicut tb ![]() bm sic
bm sic ![]() tb
tb ![]()
![]() tbm et sicut
tbm et sicut ![]() tb
tb ![]()
![]() tbm sic
tbm sic ![]() eb
eb ![]()
![]() bc quandoquidem singula singulorum quadrantes86, per 3am huius. Ideo sicut
bc quandoquidem singula singulorum quadrantes86, per 3am huius. Ideo sicut ![]() eb
eb ![]()
![]() bc sic tb
bc sic tb ![]() bm.
bm.
Sed per 12am vel 21am [A:43r] praecedentis, sicut tb ![]() bm sic
bm sic ![]() thb
thb ![]()
![]() ha igitur sicut
ha igitur sicut ![]() thb
thb ![]()
![]() ha sic
ha sic ![]() eb
eb ![]()
![]() bc.
bc.
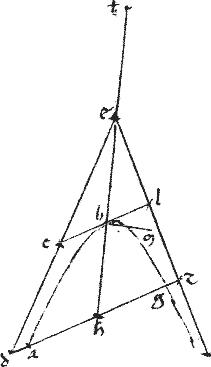
Item propter ![]()
![]() ebc ehd similitudinem sicut
ebc ehd similitudinem sicut ![]() eb
eb ![]()
![]() bc sic
bc sic ![]() eh
eh ![]()
![]() hd87.
hd87.
Ergo sicut ![]() eh
eh ![]()
![]() hd sic
hd sic ![]() thb
thb ![]()
![]() ha.
ha.
// Itaque quoniam totum ![]() eh
eh ![]() totum
totum ![]() hd est sicut ablatum
hd est sicut ablatum ![]() thb
thb ![]() ablatum
ablatum ![]() ha.
ha.
Ideo per 19am quinti Euclidis reliquum ![]() be
be ![]() reliquum
reliquum ![]() daz sicut88 totum
daz sicut88 totum ![]() eh
eh ![]() totum
totum ![]() hd et ideo sicut
hd et ideo sicut ![]() eb
eb ![]()
![]() bc.
bc.
|
Igitur per 9am 5i Euclidis ![]() daz aequale est
daz aequale est ![]() bc.
bc.
Sed per 3am huius ![]() bc quadrans est
bc quadrans est ![]() tbm.
tbm.
// Ergo et ![]() daz quadrans erit eiusdem
daz quadrans erit eiusdem ![]() tbm. // Et simili processu, vel quoniam90 per 8am huius gz da aequales, demonstrabimus, quod91 et92
tbm. // Et simili processu, vel quoniam90 per 8am huius gz da aequales, demonstrabimus, quod91 et92 ![]() dgz quadrans erit eiusdem speciei tbm sub ipsis tb bm sectionis diametris93 contentae. Quod erat demonstrandum.
dgz quadrans erit eiusdem speciei tbm sub ipsis tb bm sectionis diametris93 contentae. Quod erat demonstrandum.
Manifestum est ergo, quod si duae lineae aequidistantes et94 hyperbolen secantes utrique non tangentium95 coincidant, quod sub unius portionibus ad periferiam continuatis continetur rectangulum, aequale erit sub portionibus alterius ad periferiam similiter contiguis contento rectangulo.