[A:27v] 45a Si hyperbolen, vel ellipsim, vel circuli periferiam linea tangens coincidat secundae diametro: et a tactu ducatur quaedam linea ad648 eandem649 diametrum aequidistans650 alteri diametro: et per centrum et tactum linea producatur651: et a relicto, ut contingit, in sectione puncto agantur652 duae lineae ad secundam diametrum, haec quidem penes653 tangentem: illa vero penes654 aequidistantem diametro; factum sub ipsis triangulum maius erit655 quam triangulum abscisum656 a producta per centrum tactumque, in triangulo, cuius basis tangens, summitas autem centrum sectionis, in hyperbole: at657 in ellipsi658 et circulo, factum sub iisdem actis triangulum, cum // triangulo absciso659, aequale est triangulo, cuius basis tangens, summitasque660 centrum sectionis.
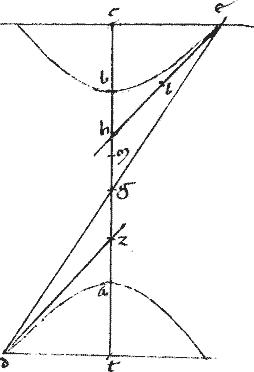
Sit hyperbola, ellipsis, vel circulus abg. // Cuius prima diametros at. // Altera td. // Centrum t. // Tangens lgm. // Tactus punctum g. // Ipsa gd aequidistans661 ipsi at. // Et662 coniuncta gt. // A quovis relicto in periferia663 puncto b agantur duae lineae usque ad td664 productam, quae [[sunt]]665 be penes666 ipsam lgm667 tangentem: et bz penes668 ipsam gd in[S:38]cidens ipsi gt apud h punctum.
|
|
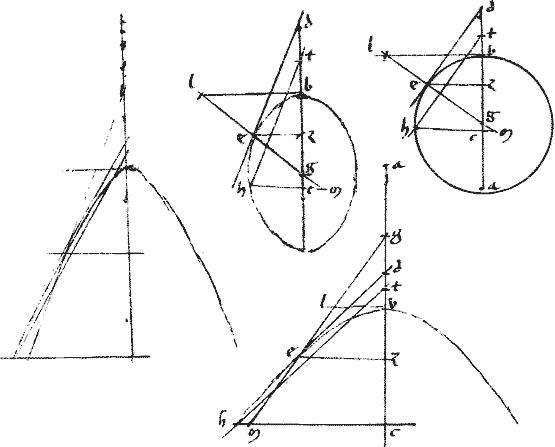
// Ducantur enim gc bn penes669 ipsam dt ordinate scilicet ductae, namque670 secunda diametros semper est ex numero ordinate ductarum ad primam.
// Eritque per 19am671 huius ratio gc ![]() ct composita ex duabus rationibus672
7
[[sic]]
ct composita ex duabus rationibus672
7
[[sic]]
| . |
// Verum [A:28r] ![]() gdl est species673 ex ct // Atque
gdl est species673 ex ct // Atque ![]() gct vel gdt est species674 ex gc sive dt.
gct vel gdt est species674 ex gc sive dt.
// Igitur per 41am huius, quandoquidem [[quod]]675 ibi affirmantur de parallelogrammis, idem sequitur676 de triangulis, quae sub illis677 assignata678 conditione sunt parallelogrammorum dimidia.
|
|
|
// In ellipsi autem
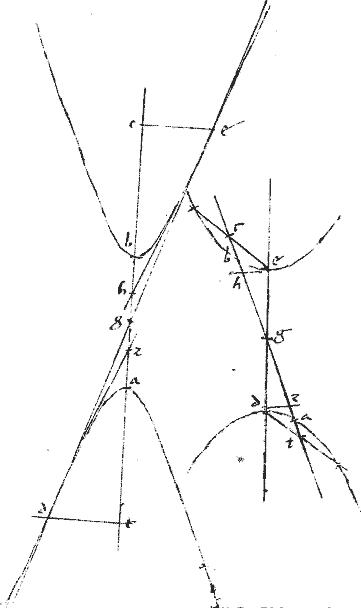
et circulo
|
// Igitur utrobique ![]() tgl aequale est
tgl aequale est ![]() lo ex at simili
lo ex at simili ![]() gdl.
gdl.
// Et quoniam propter aequidistantiam linearum ![]() bze simile679
bze simile679 ![]() lo gdl et
lo gdl et ![]() hzt simile
hzt simile ![]() lo gdt ideo, sicut td
lo gdt ideo, sicut td ![]() dg sic tz
dg sic tz ![]() zh et sicut gd
zh et sicut gd ![]() dl sic bz
dl sic bz ![]() ze.
ze.
|
|
// Rursum ergo per 41am huius, in hyperbola ![]() bze aequale est
bze aequale est
|
//
| In ellipsi autem et circulo |
|
Scholium
Oportuit682 tam hyperboles, quam, ellipseos et circuli descriptionem tripliciter variari683 pro vario situ puncti b utcumque relicti.