21a Si ab hyperboles, ellipseos, vel circuli periferia lineae ducantur ordinate ad diametrum; erunt ex ipsis quadrata ad contentas superficies294 sub receptis ad ipsis usque ad terminos transversi late[A:12v]ris speciei, ut speciei rectum latus ad transversum: itemque ad invicem ipsa quadrata, ut inter se contentae superficies sub receptis lineis, ut dictum est.
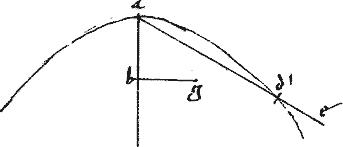
Sit hyperbole, ellipsis, circulusve, cuius diameter ab. // Et ag ad quam possunt ductae. // Ut scilicet295 ab sit transversum: ag vero rectum speciei latus. // Et a relictis contingenter in periferia punctis dz ordinate ducantur ad diametrum de zh.
// Dico iam quod ![]() zh
zh ![]()
![]() ahb atque etiam
ahb atque etiam ![]() de
de ![]()
![]() aeb est sicut ag
aeb est sicut ag ![]() ab.
ab.
Quodque ![]() zh
zh ![]()
![]() de sicut296
de sicut296 ![]() ahb
ahb ![]()
![]() aeb.
aeb.
// Coniungatur enim bg. // Et penes ag ducantur et hc. // Eritque per 12am vel 13am huius ![]() zh297 aequale
zh297 aequale ![]() cha. // Et
cha. // Et ![]() de aequale
de aequale ![]() aet. // Et quoniam propter similitudinem
aet. // Et quoniam propter similitudinem ![]()
![]() ch
ch ![]() hb sicut298 ga
hb sicut298 ga ![]() ab. // Et per primam 6i Euclidis sicut ch
ab. // Et per primam 6i Euclidis sicut ch ![]() hb sic
hb sic ![]() cha
cha ![]()
![]() bha. // Ideo et
bha. // Ideo et ![]() zh
zh ![]()
![]() bha sicut299 ga
bha sicut299 ga ![]() ab. // Eodemque argumento
ab. // Eodemque argumento ![]() de
de ![]()
![]() aeb sicut300 ga
aeb sicut300 ga ![]() ab. Quod prima proponebatur demonstrandum. // Deinde, quoniam per primam 6i praedictam. Sicut te
ab. Quod prima proponebatur demonstrandum. // Deinde, quoniam per primam 6i praedictam. Sicut te ![]() eb sic
eb sic ![]() aet
aet ![]()
![]() aeb et ideo sicut ga
aeb et ideo sicut ga ![]() ab. // Ideo et
ab. // Ideo et ![]() 301 de
301 de ![]()
![]() aeb Et ideo sicut ga
aeb Et ideo sicut ga ![]() ab. // Ideo et302
ab. // Ideo et302 ![]() de
de ![]()
![]() aeb sicut ga
aeb sicut ga ![]() ab. Et perinde sicut
ab. Et perinde sicut ![]() zh
zh ![]()
![]() bha sic
bha sic ![]() de
de ![]()
![]() aeb. // Propterea et permutatim erit
aeb. // Propterea et permutatim erit ![]() zh
zh ![]()
![]() de sicut
de sicut ![]() bha
bha ![]()
![]() aeb. // Quod supererat303 demonstrandum.
aeb. // Quod supererat303 demonstrandum.
* LEMMA
Ex ordinate ductis ad diametrum sectionis, minor est, quae propinquior summitati sectionis. Et in ellipsi et circulo, linearum ordinate ductarum maxima est secunda diametros. Nam pro parabola, in descriptione precedentis dz maior quam304 ge quandoquidem [A:13r] ![]() dz
dz ![]()
![]() ge fuit sicut za
ge fuit sicut za ![]() ae. Ideoque maius
ae. Ideoque maius ![]() dz quam
dz quam ![]() ge. // Itemque pro hyperbola, in descriptione praesentis, zh maior quam305 de quandoquidem
ge. // Itemque pro hyperbola, in descriptione praesentis, zh maior quam305 de quandoquidem ![]() zh
zh ![]()
![]() de fuit sicut
de fuit sicut ![]() ahb
ahb ![]()
![]() aeb. Ideoque maius
aeb. Ideoque maius ![]() zh quam
zh quam ![]() de. // In ellipsi autem aut circulo sit in diametro ab centrum l. Ita ut zh de sint ad eamdem partem centri, eritque similiter zh maior quam de [S:21] quae propinquior, summitati a[[,]] quandoquidem
de. // In ellipsi autem aut circulo sit in diametro ab centrum l. Ita ut zh de sint ad eamdem partem centri, eritque similiter zh maior quam de [S:21] quae propinquior, summitati a[[,]] quandoquidem ![]() zh
zh ![]()
![]() de sicut306
de sicut306 ![]() ahb
ahb ![]() 307
307 ![]() aeb maiusque sit, per 5am 2i Euclidis
aeb maiusque sit, per 5am 2i Euclidis ![]() ahb quam
ahb quam ![]() aeb (quoniam scilicet h punctum propinquius puncto l bifariae sectionis)308. Ideoque
aeb (quoniam scilicet h punctum propinquius puncto l bifariae sectionis)308. Ideoque ![]() zh maius quam
zh maius quam ![]() de.
de.
// Unde in ellipsi, aut circulo, quoniam ![]() lineae ordinatae ductae per l punctum309 ad
lineae ordinatae ductae per l punctum309 ad ![]() zh est iam, sicut
zh est iam, sicut ![]() alb
alb ![]()
![]() ahb estque per 5am 2i praedictam, maius
ahb estque per 5am 2i praedictam, maius ![]() alb
alb ![]() lo ahb. // Ideo
lo ahb. // Ideo ![]() ordinatae ductae per l hoc est 2ae diametri maius quam310
ordinatae ductae per l hoc est 2ae diametri maius quam310 ![]() zh. // Et perinde 2a diametros maxima est ordinate ductarum ad diametrum ab. Quod supererat demonstrandum.
zh. // Et perinde 2a diametros maxima est ordinate ductarum ad diametrum ab. Quod supererat demonstrandum.
LEMMA
Item in ellipsi aut circulo duae lineae aequaliter a centro remotae ordinatae ad diametrum ductae sunt invicem aequales.
Ut si in diametro ellipsis aut circuli, capiantur, puncta l m311 aequaliter a centro l remota; erit zh aequalis ei, quae per m punctum ordinate ducitur ad diametrum ab. // Nam tales lineae sunt ad312 invicem sicut ![]()
![]() ahb bma sed haec aequalia313, quandoquidem latera singula singulis aequalia supponuntur: igitur et
ahb bma sed haec aequalia313, quandoquidem latera singula singulis aequalia supponuntur: igitur et ![]()
![]() ta ipsius zh et ductae per m punctum, ad invicem aequalia: et perinde linae ipsae aequales.
ta ipsius zh et ductae per m punctum, ad invicem aequalia: et perinde linae ipsae aequales.