[S:16] 14a Si superficies conicae ad verticem positae plano secentur non per vertices; erit utraque187 superficierum sectio vocata hyperbole: et duarum sectionum diameter eadem erit: et188 ipsae, ad quas poterunt ductae ad diametrum aequidistantes ei, quae in basi coni, lineae aequales: et speciei transversum latus commune inter summitates sectionum. Vocenturque tales sectiones contrapositae.
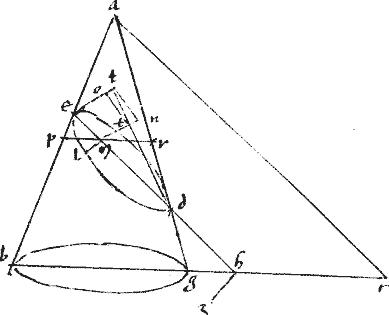
Conicae superficies ad verticem a positae plano non per verticem secentur: sintque in superficiebus factae sectiones dez htc 189.
Dico primum quod utraque sectionum dez h ![]() c est hyperbole.
c est hyperbole.
Sit enim circulus bdgz per quem fertur linea describens.
Et ducatur ipsi bdg circulo, aequidistans planum in altera superficie, per puncta xhoc quae, per 4am huius erunt in periferia circuli. [A:9r]
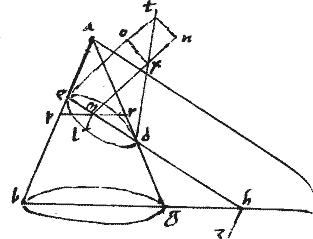
Eruntque per 16am 11i Euclidis ipsae rectae zd hc quae sunt secantis plani et circulorum comunes sectiones; invicem aequidistantes.
Sint autem centra circulorum ly axis autem conicae superficiei lay. // Et ab l ad zd cathetus lm 190 extendatur, utrinque ad periferiam circuli ad puncta b, g.
Et per bg et axim planum ducatur faciens in circulis lineas xo bg per16am 11i, aequidistantes in superficiebus autem lineas bao gax per 3am huius.
Et quoniam bg est ad rectos ipsi zd ideo per 10am 11i .
Et ipsa xo ad rectos erit ipsi hc incidens ad punctum n quoniam scilicet haec sunt illis aequidistantes singulae singulis.
Item plani facientis hyperbolas191 et plani per axem communis sectio sit recta mn secans hyperbolarum periferias apud e ![]() 192 puncta in ipsis conicis superficiebus. Ita ut me
192 puncta in ipsis conicis superficiebus. Ita ut me![]() n puncta sint in recta193.
n puncta sint in recta193.
Demum in ipso eodem plano per axem, in quo videlicet iacent ![]()
![]() bag oax
bag oax
ducatur ipsi mn aequidistans sat194. // Et sicut ![]() as195
as195 ![]()
![]() bsg196 sic sit
bsg196 sic sit ![]() e
e ![]() ep ad rectos. Itemque sicut
ep ad rectos. Itemque sicut ![]() at
at ![]()
![]() [[etx]] sic sit
[[etx]] sic sit ![]() e
e ![]()
![]() r ad rectos.
r ad rectos.
Et quoniam propter linearum aequidistantiam et ![]()
![]() similitudinem
similitudinem ![]() as197
as197 ![]()
![]() bsg198 sicut199
bsg198 sicut199 ![]() at
at ![]()
![]() otx200. Ideo
otx200. Ideo ![]() e
e ![]() ep sicut
ep sicut ![]() e
e ![]()
![]() r.
r.
Quare per 9am 5i Euclidis aequales sunt ad invicem ipsae ep ![]() r.
r.
Patet ergo per 12am praemissam201 quod dez htc202 sectiones sunt hyperbole, quod erat primum. Quodque mn est utrique pro diametro, quod erat secundum: quodque ep tr203 ad quas possunt ordinate, et quae rectae diametri204 sunt invicem aequales205. Quod erat tertium. Quodque et206 transversa diameter communis est utrique sectioni: quod fuit postremum ex demonstrandis.
Quae quidem sectiones sic factae, easque sortitae conditiones contrapositae vocantur207.