13^a Si conus plano secetur per axim: secetur autem et altero plano coincidente utrique laterum trianguli per axim, neque ducto penes basim coni, neque subcontrarie: planum autem, in quo est basis coni, et secans planum coincidant¹⁶¹ ad rectam ad rectos¹⁶² existentem vel basi trianguli per axim, vel in rectam¹⁶³ ipsi; quae a sectione coni aequidistans ducitur comuni sectioni planorum usque ad diametrum sectionis, poterit,quod superficies adiacens¹⁶⁴ ad quamdam lineam, ad quam habet rationem diameter sectionis, quam quadratum quod sit a ducta a vertice coni penes diametrum [S:15] sectionis, usque ad occursum basis trianguli ad contentum sub tota linea (quae constat ex basi et adiuncta occurrente) et sub ipsa occurrente¹⁶⁵: et latitudinem habens recepta sub ipsa a diametro¹⁶⁶ ad summitatem sectionis, deficiens specie¹⁶⁷ simili et similiter posito, contento sub diametro et illa, ad quam possunt ductae ordinate. Vocetur autem talis sectio, ellipsis, sive defectio.

[A:8r]

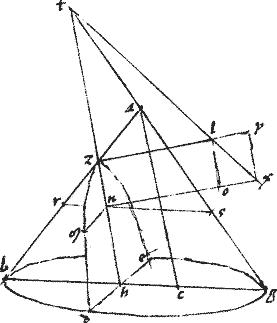
Conus, cuius vertex a basisque circulus bg secetur plano per axem: sitque sectio per 3^am abg. Secetur et altero plano secante basim coni per rectam zh ad rectos ipsi bg vel eidem in rectum productae, et coincidente lateribus trianguli abg et nec aequidistante basi coni, nec subcontrarie ducto, et faciente in conica superficie sectionem dle per 9^am. // Item agatur ac¹⁶⁸ penes ed coincidens ipsi bg apud c¹⁶⁹ . // Sitque et ad rectos ipsi ed ita ut de et. Sit sicut ac¹⁷⁰ ad rectangulum bcg¹⁷¹. // Et a contingenti puncto sectionis l agatur ad diametrum lm penes zh. Et connexa dt compleantur ^la etmn xnto.

Dico iam quod lm potest ex adiacens ad et sub latitudine em et deficiens specie xt simili ^lo det.

Nam ducta pmr penes bg iam per 24^am 6ⁱ¹⁷² Euclidis ratio ac¹⁷³ bcg¹⁷⁴ componitur

ex rationibus ac cb cg 175 .

Et propter similitudinem et proportionem laterum. Eadem ratio componetur ex rationibus eh hb atque dh hg. Et similiter eadem componetur ex rationibus em mp atque dm mr.

Sed per 24^am176 praedictam.

Ratio emd pmr. Componitur ex rationibus em mp dm¹⁷⁷ mr.

Igitur emd pmr sicut¹⁷⁸ ac bcg¹⁷⁹. Et ideo sicut de et et sicut dm mx propter ¹⁸⁰ similitudinem.

Verum per primam 6ⁱ dm mx sicut¹⁸¹ dme emx.

Igitur dme emx sicut¹⁸² emd pmr.

Quare per 9^am 5ⁱ pmx aequale est emx.

Cumque per 15^am 11ⁱ planum, in quo pr lm aequidistet basi bg ideo per 4^am huius [A:8v]

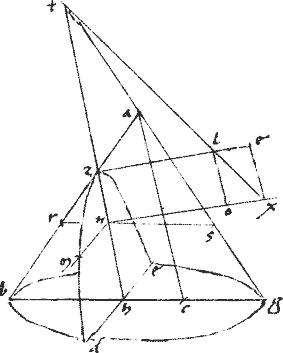
puncta p l r sunt in periferia circuli, cuius diameter pr.

Et ideo per 8^am 6ⁱ¹⁸³ pmr aequum est lm.

Quare et lm aequum erit emx.

Quod erat demonstrandum.

Vocetur autem talis sectio ellipsis sive defectio: et ipsa et ad quam possunt ductae ad de ordinate: et eadem recta. Transversa autem de. Item det [[species]]¹⁸⁴. Et manifestum est quod dme emx: hoc est ad lm est¹⁸⁵ sicut dm mx vel de et videlicet sicut transversum ad rectum speciei latus. Item patet, quod secunda diametros ellipsis est media proportionalis inter transversum et rectum speciei latus: hoc est inter ipsas de et. Namque¹⁸⁶ dimidium secundae diametri potest , quod sub dimidio transversi et dimidio recti. Quare tota poterit sub totis contentum.