[A:6v]

11^a Si conus plano secetur per axim, secetur autem et altero plano secante basim coni per rectam ad rectos existentem basi trianguli per axim: et diameter sectionis aequidistans sit uni laterum trianguli per axim; quae a sectione coni ducitur aequidistans communi sectioni secantis plani et basis coni usque ad dia[S:13]metrum sectionis, poterit contentum sub recepta sub¹²² ipsa a¹²³ diametro ad summitatem sectionis, et sub alia quadam linea, quae rationem habet ad eam, quae inter coni angulum est et summitatem sectionis, quam¹²⁴ habet quadratum, quod a basi trianguli per axim, ad comprehensum sub reliquis duobus trianguli lateribus. Vocetur autem talis sectio parabole .

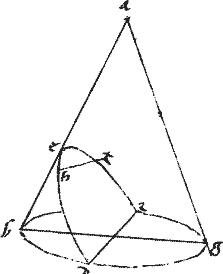
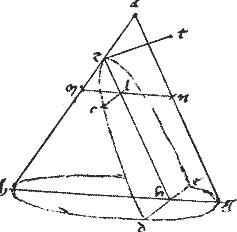
Conus, cuius vertex a basis bg circulus, secetur plano per axim, sitque sectio per 3^am abg. Secetur et altero plano secante basim coni per rectam de ad rectos ipsi bg et faciente in conica superficie sectionem dze cuius diameter zh aequidistet uni laterum ut pote¹²⁵ ag. // Et zt ad rectos ipsi zh ita ut zt za sit sicut bg bag. Et a contingenti¹²⁶ puncto in periferia sectionis, ut c agatur penes ipsam de ad diametrum zh recta linea cl.

Dico quod cl aequale est tzl.

Ducatur enim in plano linea¹²⁷ mln aequidistans bg.

Eritque per 24^am 6ⁱ¹²⁸ et ex similitudine¹²⁹ triangulorum¹³⁰ ratio bg bag¹³¹

composita est132 ex rationibus bg ga ba .

Et ideo ex rationibus mn na mn ma .

Nec secus ex rationibus ml lz mz .

Quare ex rationibus ml lz ln za .

Propter proportiones videlicet laterum et segmentorum.

Sed adhuc¹³³ per 24^am 6ⁱ¹³⁴ Euclidis ratio lmn¹³⁵ lza componitur

ex rationibus ml lz ln za .

Igitur lmn rectangulum lza sicut¹³⁶ bg bag et ideo sicut zt za. Sed per primam 6ⁱ Euclidis sicut zt za sic tzl lza.

Ergo sicut tzl lza. Sic lmn lza.

Quare per 9^am 5ⁱ tzl aequale lmn .

Verum cum planum, in quo mlc¹³⁷ per 15^am 11ⁱ Euclidis aequedistet circulo bdg atque ideo per 4^am huius, puncta mcn sunt in periferia circuli cuius diameter mn.

Propterea per 8^am 6ⁱ¹³⁸ mln aequum¹³⁹ erit ¹⁴⁰ cl.

Igitur et cl aequum erit tzl.

Quod erat demonstrandum.

Vocetur autem talis sectio parabole. Ipsa autem tz ad quam possunt ductae ordinate ad zh diametrum: voceturque¹⁴¹ et recta. Et manifestum est quod cl semper media proportionalis est inter lz zt.