PROPOSITIO IX

68 Si lineae quotcumque continuatim sese excedentes excessu aequali disponantur, quadrata longissimae uno pauciora, quam lineae ad quadrata linearum sese excedentium, dempta brevissima minorem rationem habebunt, quam habet quadratum longissimae ad duo haec simul, scilicet ad contentum sub longissima, brevissimaque una cum tertia parte quadrati eius, qua longissima excedit brevissimum, ad quadrata vero linearum sese excedentium, dempta longissima, habebunt maiorem praedicta rationem.

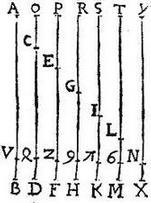
69 Sint quotquot lineae AB, CD, EF, GH, IK, LM, NX sese excedentes excessu aequali. His suppleantur OC, PE, RG, SI, TL, YN, ut sint OD, PF, RH, SK, [S:203] TM, YX, singulae ipsi AB longissimae aequales. 70 Est ostendendum quod quadrata AB, OD, PF, RH, SK, TM simul ad quadrata AB, CD, EF, GH, IK, LM, minorem rationem habent, quam quadratum AB ad rectangulum AB in NX cum tertia parte quadrati NY, sed ad quadrata CD, EF, GH, IK, LM, NX maiorem rationem eadem. 71 Nam sicut quadratum AB ad rectangulum AB in BV cum tertia parte quadrati AV, sic iam sunt quadrata OD, PF, RH, SK, IM, YX ad rectangulum sub NX, et sub composita ex OD, PF, RH, SK, TM, YX una cum triente quadratorum OQ, PZ, R9, S, T6, YN (positis scilicet BV, DQ, ZF, 9H, K, 6M singulis aequalibus ipsi NX) itaque si ostenderimus rectangulum ex NX in compositam praedictam una cum triente quadratorum dictorum minus esse, quam quadrata AB, CD, EF, GH, IK, LM simul sumpta: maius vero quam quadrata CD, EF, GH, IK, LM, NX simul sumpta propositum ostensum erit. Sic vero ostendetur. 72 Nam, per 2^<am> secundi Elementorum⁹, rectangulum NX in compositam ex OD, PF, RH, SK, TM, YX una cum triente quadratorum OQ, PZ, R9, S, T6, YN aequalia sunt quadratis QD, ZF, 9H, K, <6M, NX una cum rectangulo NX in compositam ex OQ, PZ, R9, S,¹⁰> T6, YN; et triente quadratorum OQ, PZ, R9, S, T6, YN. 73 At vero, per 4^<am> secundi Elementorum, quadrata AB, CD, EF, GH, IK, LM aequalia sunt quadratis VB, QD, ZF, 9H, K, 6M, una cum rectangulo BV, in duplam harum scilicet AV, CQ, EZ, G9, I, L6, et quadratis eorumdem, communia itaque sunt utrobique quadrata linearum aequalium NX.

74 Sed rectangulum NX in compositam ex OQ, PZ, R9, S, T6, YN minus est quam rectangulum VB in duplam harum, scilicet AV, CQ, EZ, G9, I, L6. Quandoquidem hae lineae sunt aequales his CO, EP, GR, IS, LT, NY residuis autem maiores et per corollarium praemissae, quadrata AV, CQ, EZ, G9, I, L6, maius sunt quam tertia pars quadratorum OQ, PZ, R9, S, T6, YN. 75 Igitur quadrata AB, CD, EF, GH, IK, LM, simul maius sunt quam rectangulum NX in compositam ex OD, PF, RH, SK, TM, YX una cum triente quadratorum OQ, PZ, R9, S, T6, YN, superest nunc ostendere, quod quadrata CD, EF, GH, IK, LM, NX minus sunt quam rectangulum NX in compositam praedictam una cum triente quadratorum praedictorum. 76 Rursum itaque, per 4^<am> secundi Elementorum, quadrata CD, EF, GH, IK, LM, NX aequantur quadratis CQ, EZ, G9, I, L9, et quadratis QD, ZF, 9H, K, 6M, NX, et rectangulo NX in duplam harum simul CQ, EZ, G9, I, L6. 77 Communia sunt utrobique quadrata QD, ZF, 9H, K, 6M, NX. Sed rectangulum NX in compositam ex OQ, PZ, R9, S, T6 YN maius est quam rectangulum NX in duplam harum simul CQ, EZ, G9, I, L6. 78 Et quadrata OQ, PZ, R9, S, T6, XN per corollarium praemissae, maius sunt quam triplum quadratorum CQ; EZ, G9, I, L6. 79 Igitur quadrata CD, EF, GH, IK, LM, NX minus sunt quam rectangulum NX in compositam ex OD, PF, RH, SK, TM, YZ cum triente quadratorum OQ, PZ, R9, S, T6, YN. Quare constat propositum.

SCHOLIUM

80 Suppositis autem iisdem, eodemque modo dispositis lineis, si similes formae, similiterque describantur ab his, quae sese excedunt, et ab his, quae aequales sunt longissimae, tunc et formae, quae ab aequalibus longissimae describentur, minorem rationem habebunt ad formas linearum sese excedentium (dempta brevissima) quam quadratum longissimae ad haec duo simul, scilicet ad contentum sub longissima et brevis[S:204]sima, et ad tertiam partem quadrati lineae, qua¹¹ longissima brevissimam excedit: ad formas autem earumdem linearum (dempta longissima) rationem habebunt dicta maiorem. Nam similes formae sunt quadratis super easdem lineas descriptis proportionales.