PROPOSITIO VIII
48 Si lineae quotcumque crescant eodem excessu, qui sit aequalis minimae, tunc quadrata uno plura facta ex maxima una cum contento sub minima, et sub congerie linearum crescentium, triplum conficiunt aggregati quadratorum a singulis crescentibus factorum.
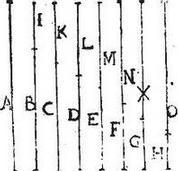
49 Sint quotvis lineae ut puta A, B, C, D, E, F, G, H continuo, et aequali excessu sese excedentes; sitque excessus aequalis ipsi H minimae. His autem omnibus (excepta A maxima) <a>diiciantur totidem lineae singulae singulis aequales7, sed converso ordine, ut minima maximae, et vicissim maxima minimae adiiciantur: hoc est I aequalis ipsi H adiiciatur ipsi B, K aequalis G adiiciatur ipsi C, L aequalis F adiiciatur ipsi D, M aequalis E adiiciatur eidem E, N aequalis D adiiciatur ipsi F, X aequalis C adiiciatur ipsi G, O aequalis B adiiciatur H. 50 Sic omnes lineae, ex his adiectionibus conflatae, erunt singulae aequales A longissimae. 51 Est igitur ostendendum, quod quadrata ex his lineis aequalibus omnibus A, BI, CK, DL, EM, FN, GX, HO cum quadrato ipsius A, una cum rectangulo ex H minima in congeriem ipsarum A, B, C, D, E, F, G, H, triplum faciunt quadratorum ab ipsis A, B, C, D, E, F, G, H, singulis factorum. [S:201]
52 Hoc modo per 4<am> secundi Elementorum toties sumptam quot sunt lineae.
|
53 Ecce igitur quadrata A, B, C, D, E, F, G, H cum quadratis I, K, L, M, N, X, O; cumque quadrato A, omnia haec dupla sunt quadratorum A, B, C, D, E, F, G, H. Quare ad concludendum propositum superest demonstrare, quod reliqua supplementa una cum contento sub H et linea aequali omnibus A, B, C, D, E, F, G, H lineis, sunt aequalia cumulo quadratorum A, B, C, D, E, F, G, H. Hoc enim ostenso statim astruitur propositum.
54 Ostendendum est, inquam, quod rectangula BI, CK, DL, EM, FN, GX, HO una cum rectangulo H in aggregatum ex lineis A, B, C, D, E, F, G, H, sunt aequalia quadratis A, B, C, D, E, F, G, H simul.
|
55 Et similiter, quaecumque supplementa duplicata aequalia essent contento sub minima, et multiplici cuiuslibet secundum partes numeros sequentes. 56 Adde utrobique rectangulum H in lineam aequalem omnibus A, B, C, D, E, F, G, H: eruntque dupla rectangulorum BI, CK, DL, EM, FN, GX, HO, rectangulo ex H in factam ex A, B, C, D, E, F, G, H, aequalia contento rectangulo sub H, et sub linea facta ex omnibus his, a tripla B, quincupla C, septupla D, nonupla E, undecupla F, tredecupla H, et sic deinceps multiplici secundum impares numeros sequentes. 57 Sed quadratum A aequale est rectangulo H in aggregatum ex omnibus aequalibus ipsi A, quoties enim H ipsam A, toties A mensurat dictum aggregatum, et ideo quadratum A aequale est rectangulo H in factam ex A duploque ipsarum B, C, D, E, F, G, H. Quandoquidem tale duplum facit omnes aequales ipsi A dempta ipsa A.
|
|
[S:202] 59 Quare constat quadrata ipsarum A, B, C, D, E, F, G, H simul aequalia esse rectangulo sub H contento et sub composita ex his omnibus, scilicet ex A triplo B, quincuplo C, septuplo D, nonuplo E, undecuplo F, tredecuplo G, quindecuplo H, et deinceps multiplici per impares, ubi opus fuerit sequentes. Fuit vero tale rectangulum contentum sub H, dictaque composita iam aequale duplis rectangulum BI, CK, DL, EM, FN, GX, HO, una cum rectangulo H in compositam ex A, B, C, D, E, F, G, H. 60 Igitur dupla rectangula BI, CK, DL, EM, FN, GX, HO una cum rectangulo H in compositam ex A, B, C, D, E, F, G, H, aequalia erunt aggregato quadratorum A, B, C, D, E, F, G, H, quod restabat demonstrandum.
COROLLARIUM
61 Igitur manifestum est, quadrata simul omnia linearum aequalium longissimae, quadratis simul omnibus linearum sese aequaliter excedentium, minus quam tripla esse. Quandoquidem assumptis quibusdam tripla efficiuntur illis. 62 Reliquis vero, dempto longissimae quadrato plusquam tripla inveniuntur: quandoquidem assumpta ipsa sunt minus quam tripla ad quadratum longissimae. Quod et verum erit de similibus similiterque constitutis super ipsas lineas formis: quandoquidem similes species sunt in ratione quadratorum.
SCHOLIUM
63 Notandum quod, id quod presens octava demonstrat de lineis, referri potest ad numeros ipsis lineis proportionales. Quidquid enim de ductu ex ratione linearum agitur, potest ad numeros transferri: sicut et vicissim quidquid de ductu et ratione numerorum demonstratur, idem omnino de lineis concludi potest. 64 Itaque ex hac octava elicitur haec regula progressionis. Sunto quotvis numeri per crementum primae crescentes. Capiatur quadratum maximi, et multiplicetur semel pluries, quam sunt numeri, et producto adiiciatur is numerus, qui fit ex ductu minimi in aggregato omnium numerorum. 65 Compositum autem ex additione secetur in tria, nam tertia pars est aggregatum quadratorum ab assumptis numeris singulis factorum. Exempli gratia 1, 2, 3, 4, 5, horum quadrati 1, 4, 9, 16, 25. Quoniam numeri assumpti sunt quinque, capiatur sexies numerus quadratus maximus scilicet 25, et fiunt 150; ex minimo in aggregatum assumptorum, hoc est ex 1 in 15, fiunt 15. 66 Hic adiectus 150, facit 165, huius pars tertia 55 congeries scilicet quadratorum8. Rursum sint assumpti numeri 3, 6, 9, 12, 15 horum vero quadrati 9, 36, 81, 144, 225, maximus 225 sexies facit 1350. 67 Productum ex 3 in 45 congeriem assumptorum scilicet 135 adiectus ipsi 1350 facit 1485, huius tertia pars 495 congeries quadratorum.