PROPOSITIO X

81 Si ad spiralem lineam in quavis circumvolutione descriptam ab initio spirae, ducantur quotquot rectae continentes angulos aequales, ipsae sese continuatim aequaliter excedent.

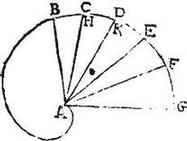
82 Esto spiralis linea cuius initium A, peripheria BCD, ad quam AB, AC, AD, AE, AF, AG lineae rectae sint ductae compraehendentes singulae duae laterales angulos aequales. Aio quod AB minor est quam AC, et AC minor quam AD, et AD minor quam AE, eodem excessu, et sic deinceps. 83 Nam ex diffinitione spiralis lineae, linea AB brevior quam AC, et AC brevior quam AD. Abscinditur ex AC ipsi AB, aequalis AH, deque AD ipsi AC aequalis AK. Itaque, quo tempore linea AB permeavit in AC, eodem et AC linea permeavit in AD. 84 Nam, ex diffinitione, linea circumducta aequalibus temporibus, aequales angulos pertransit. Sed, in iisdem temporibus, punctum describens spiram pertransit spatium HC et inde spatium KD. 85 Igitur, per 2^<am> huius, spatia HC, KD sunt angulis BAC, CAD proportionalia. Sed per hypothesim, aequales sunt anguli, aequalia igitur sunt spatia HC, HD, qui sunt excessus linearum, et similiter alii excessus aequales ostendentur.

86 Vel sic quoniam punctum describens spiram pertransit spatia HC, KD in temporibus aequalibus, quibus utique linea AB permeat angulos aequales et, per primam huius, spatia HC, KD sunt temporibus proportionalia, propterea spatia sunt invicem aequalia.

87 Vel sic quoniam puncti praedicti motus supponitur uniformis ex diffinitione, ideo spatia HC, KD aequalibus peracta temporibus a puncto sunt aequalia, quod propositum est. Idemque de reliquis excessibus.

88 Quod si lineae deductae ab initio spirae compraehendant aequales circumferentias de circulo super initium spirae descripto, idem sequitur, ut linearum excessus sint inter se aequales, nam anguli super aequales circulorum peripherias ad centrum constituti sunt, per 27^<am> tertii Elementorum, aequales.