PROPOSITIO XXXI.

Si circulus sphaeram secet, sphaericorum segmentorum utrumlibet aequum est cono, cuius basis est secans circulus, celsitudo vero ea recta, quae sic se habet ad axem ipsius segmenti, sicut aggregatum ex semidiametro sphaerae, et ex axe reliqui segmenti ad eundem axem.

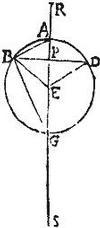
Esto sphaera ABGD, quam circa axem AG manentem revolutus semel describit semicirculus ABG, quae secetur circulo, cui recta sit diameter AG, et cuius diameter sit BD secans AG apud P. Sintque segmenta ABD, BGD, quorum axes AP, PG. sitque sicut aggregatum ex EA, PG, ad ipsam PG, sic RP ad AP: aio quod conus, cuius basis semidiameter BP, et celsitudo RP aequalis est sphaerico segmento ABD. Item sit sicut aggregatum ex EG, PA ad ipsam PA, sic SP ad GP. Aio quod conus cuius basis semidiameter BP, et celsitudo SP aequalis est sphaerico segmento BGD. Primum sic ostendo: cum EA, PG simul ad PG sit sicut RP ad AP erit disiunctim sicut EA ad PG, sic RA ad AP, et conversim, sicut PG ad EA, sic AP ad RA, et permutatim, sicut PG ad AP, sic EA ad RA: et conversim sicut AP, ad PG, sic RA ad AE; et coniunctim sicut AG ad GP, sic RE ad EA: sed AG ad GP ratio dupla est eius, quae AG ad GB per 8. sexti AG autem ad GB sicut AB ad BP, propter similitudinem triangulorum AGB, ABP: ergo ratio AG ad GP dupla est eius, quae AB ad BP; fuit autem sicut AG ad GP sic RE ad EA. Igitur ratio RE ad EA dupla est eius, quae AB ad BP sed circulus, cuius semidiameter AB ad circulum, cuius semidiameter BP duplam habet rationem eius, quam AB ad BP, (quandoquidem circuli ad invicem sunt [S:77] per 2.12. sicut quadrata diametrorum, vel semidiametrorum.) Itaque RE ad EA erit sicut circulus, cuius semidiameter AB ad circulum, cuius semidiameter BP. Quamobrem duo coni, quorum unius quidem basis semidiameter AB, et celsitudo EA, alterius autem basis semidiameter BP, et celsitudo RE sunt per 12.12. aequales invicem, quando celsitudines sunt basibus reciprocae: sed conus, cuius basis semidiameter BP, et celsitudo RE per 22. huius, aequalis est duobus conis, quorum basis semidiameter BP, et celsitudines RP, PE: conus autem, cuius basis ex centro AB, et celsitudo AE, per corollarium praemissae, aequalis est sectori sphaerico ABED. Igitur duo coni, quorum basis semidiameter BP, et celsitudines RP, PE simul sumpti sunt aequales sectori sphaerico ABED, quod est aggregatum ex segmento sphaerico ABD, et ex cono, cuius basis semidiameter BP, et celsitudo PE: auferatur ergo communis conus, cuius basis semidiameter BP, et celsitudo PE, et supererit conus, cuius basis semidiameter BP, et celsitudo RP aequalis sphaerico segmento ABD: quod erat primum ex demonstrandis: reliquum sic ostendo.

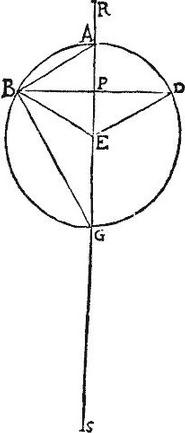
Cum EG, PA simul ad PA sit sicut SP ad GP erit disiunctim, sicut EG ad PA, sic SG ad PG; et conversim, sicut PA ad EG, sic GP ad SG, et permutatim , sicut AP ad PG, sic EG ad GS, et conversim, sicut GP ad PA, sic SG ad GE, et coniunctim, sicut GA ad AP, sic SE ad EG: sed per 8. sexti ratio GA ad AP dupla est eius, quae GA ad AB, estque sicut GA ad AB, sic GB ad BP propter similitudinem triangulorum GAB, GBP: igitur ratio GA ad AP dupla est eius, quae GB ad BP, fuit autem sicut GA ad AP sic SE ad EG, quare, et ratio SE ad EG dupla eius est, quae GB ad BP: sed circulus cuius semidiameter GB ad circulum, cuius semidiameter BP duplam habet rationem eius, quam GB ad BP, ex 2.12. Itaque SE ad EG erit sicut circulus, cuius semidiameter GB ad circulum, cuius semidiameter BP: quamobrem duo coni, quorum unius quidem basis semidiameter GB, celsitudo autem EG, alterius autem basis semidiameter BP, celsitudo autem SE sunt per 12.12. invicem aequales, (quandoquidem celsitudines sunt basibus mutae;) per praecedentis autem corollarium. conus, cuius basis semidiameter BG, celsitudo autem EG aequalis est sectori sphaerico BGDE: igitur sector sphaericus BGDE aequalis est cono, cuius basis, quidem semidiameter BP celsitudo autem SE: apponatur utrobique conus, cuius basis semidiameter BP, et celsitudo PE eritque segmentum sphaericum BGD aggregatum scilicet ex sectore BGDE, et dicto cono, aequale conis, quorum basium semidiameter BP, et celsitudines PE, ES simul sumptae: sed tales coni simul sumpti sunt per 22. aequales cono, cuius basis semidiameter BP, et celsitudo PS; ergo, et conus, cuius basis semidiameter BP, celsitudo autem PS aequalis est segmento sphaerico BGD: quod fuit reliquum ex demonstrandis: itaque vera est tota propositi sententia. [S:78]

COROLLARIUM.

Hinc manifestum est, quod sphaericum segmentum ad conum eiusdem basis, ac verticis est sicut linea constans ex semidiametro sphaerae, et axe reliqui segmenti ad ipsum axem. Namque ut paucis agam, conus BRD ad conum BAD eiusdem basis est sicut RP altitudo ad PA altitudinem, fuit autem sphaericum segmentum BAD aequale cono BRD. Atque RP linea ad lineam PA, sicut aggregatum EGP ad axem GP. Igitur sphaericum segmentum BAD ad conum BAD, sicut EGP aggregatum ad axem GP; quod est propositum. Non aliter ostendam, quod segmentum sphaerae BGD ad conum BGD erit sicut aggregatum EAP ad axem AP sicut infert corollarium.