PROPOSITIO XXX.

Si conica superficies verticem in centro sphaerae habens sphaeram in duos sectores disterminet uterlibet sectorum aequalis est cono, cuius basis aequalis est basi sphaericae ipsius sectoris, celsitudo autem aequalis semidiametro sphaerae.

De circulo ABGD, cuius centrum E, et diameter AG sumatur arcus AB, et ducatur semidiameter EB circumducto autem semicirculo ABG, stante diametro [S:75] AG describetur sphaera, et in eodem ambitu sector circuli ABE describet solidum sphaerae sectorem ABED, ponatur conus M, cuius basis aequa sit basi sphaericae sectoris ABD, quam scilicet describit arcus AB, celsitudo vero aequalis sit semidiametro AE: aio, quod aequalis est conus M sphaerico sectori ABD; nam secus erit aequalis alicui sectori maiori, vel minori: sit ergo primum aequalis conus M sectori sphaerico ZHT minori, quam est sector ABD, et cum eo concentrico, quem describat arcus ZH ipsis lineis AE, EB terminatus. Et secetur arcus AB iterum, atque iterum, donec per 13.12. arcuum chordae non contingant peripheriam ZHT; sitque una chordarum AK, et ad eum perpendicularis EL, et circumacto rectilineo AKBE circa axem AE, describatur solidum ABD, quod per praecedentem, aequale erit cono, cuius basis aequalis est conicis superficiebus per chordas AK, KB descriptis, celsitudo vero perpendiculari EL: hoc itaque cono maior est conus M, qui et basi, et celsitudine maior est; sed conus M aequalis fuit sphaerico sectori ZT: ergo sphaericus ZT maior est solido ABD: pars toto, quod est impossibile.

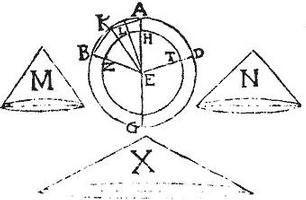
Vel sic conus M maior est solido ABD, quandoquidem maior est cono qui solido aequalis: ergo, et maior sectore sphaerico ZT: non est ergo ei aequalis, sicut supponebatur. Sit deinde conus M aequalis sectori sphaerico maiori, quam est sector ABD; sed brevitatis causa suppositus sector sit sector sphaericus ZHTE, et conus M habeat basim aequam sphaericae basi sectoris ZT, quam scilicet describit arcus ZH, et celsitudinem aequalem semidiametro EH. Aio, quod conus M non erit aequalis alicui sectori sphaerico maiori, quam est sector ZT; sit enim, si possibile est, aequalis sectori BD concentrico cum sectore ZT, et ipso maiori, quem describit sector circuli ABE, et inscribantur arcui AB chordae ut prius non tangentes circulum ZH, et circumducto rectilineo ABE, formetur solidum BD: etc. quod per praecedentem, aequale erit cono, cuius basis aequalis est conicis superficiebus per chordas AK, KB descriptis, celsitudo vero perpendiculari EL: hic ergo conus maior erit cono M, quem et basi, et celsitudine superat: sed conus M aequalis fuit per hypothesim sectori BD: igitur, et solidum BD maius est sectore BD: pars toto, quod est impossibile: non est ergo conus M aequalis alicui sectori sphaerico maiori, quam est sector ZT. Similiter si conus M supponatur habere basim aequam sphaericae basi sectoris BD, et celsitudinem aequam semidiametro AE: non erit conus M aequalis alicui sectori maiori, quam est sector BD: sed nec minori, ut fuit ostensum: superest ergo ut aequalis sit omnino conus M sectori sphaerico ABED; quod est propositum. Et quoniam sphaera ABG dissecatur in duos sectores, quos disterminat conica superficies descripta per lineam EB: poterimus hoc idem ostendere de sphaerico sectore BGD descripto per circuli sectorem EBG. Sit ergo conus N, cuius basis aequalis sit sphaericae basi sectoris BGD, quam describit arcus BG, et similiter ostendemus, quod aequalis erit conus N sectori sphaerico BGD. Vel hac via: sit conus X habens basim aequam superficiei toti sphaerae ABG, et celsitudinem aequam semidiametro AE: eritque per 25. aequalis conus X [S:76] sphaerae ABG: et basis coni X aequalis basibus conorum M, N, simul sumptis. Quapropter per 21. et conus X conis M, N, simul sumptis aequalis erit: igitur et coni M, N, simul sumpti erunt aequales sphaerae ABG: itaque de sphaera ABG sector sphaericus ABD, et de aggregato conorum M, N, conus M auferatur, aequalia ab aequalibus, et supererunt sector sphaericus BGD, et conus N aequales: quod est propositum.

COROLLARIUM.

Manifestum est ergo, quod sector sphaericus aequalis est cono, cuius basis semidiameter est aequalis lineae, quae a vertice sphaerici segmenti ad peripheriam basis, celsitudo autem aequalis semidiametro sphaerae: nam per corollarium 16. circulus, cuius semidiameter est linea, quae a vertice segmenti sphaerici ad peripheriam basis aequalis est basi sphaericae ipsius sectoris. Quare conus, cuius basis aequalis circulo, cuius diameter est linea, quae a vertice segmenti sphaerici ad periphaeriam basis, celsitudo autem aequalis semidiametro sphaera; iam aequalis erit cono, cuius basis aequalis est basi sphaericae sectoris, celsitudo autem semidiametro sphaerae: sed hic conus aequalis fuit sphaerico sectori: ergo, et ille conus, cuius basis est circulus habens semidiametrum aequalem lineae, quae a vertice segmenti sphaerici ad peripheriam basis, et celsitudinem aequalem semidiametro sphaerae, aequalis erit sphaerico sectori, sicut infert corollarium.