PROPOSITIO XXXII.

Si circulus sphaeram secet; sphaericorum segmentorum utrumlibet aequum est cono, cuius basis semidiameter est aequalis ipsius segmenti axi, celsitudo vero aequalis aggregato ex semidiametro sphaerae, et ex axe reliqui segmenti.

Repetita descriptione praecedenti: aio quod segmentum sphaericum ABD aequum est cono, cuius basis semidiameter aequalis est axi AP, celsitudo vero aggregato ex EG semidiametri, et GP axe reliqui segmenti. Item aio quod segmentum sphaericum BGD aequale est cono, cuius basis semidiameter aequalis est axi GP, celsitudo vero aequalis aggregato ex AE semidiametro, et AP axe reliqui segmenti. Primum sic ostendo; quoniam ratio GP ad PA dupla est eius, quae BP ad PA per 8. sexti cuius, et dupla est per 2.12. ratio circuli cuius semidiameter BP ad circulum, cuius semidiameter PA; ideo GP ad PA erit sicut circulus, cuius semidiameter BP ad circulum, cuius semidiameter PA: fuit autem in praemissa, sicut GP ad PA, sic EA, vel EG ad AR; et coniunctim sicut EG, GP simul ad PR totum, sic PG ad PA per 13.5.. Et ideo sicut circulus, cuius semidiameter BP ad circulum, cuius semidiameter PA. Quamobrem duo coni, quorum unius quidem basis semidiameter est AP, et celsitudo aggregatum ex EG, GP, alterius vero basis semidiameter BP, et celsitudo PR sunt aequales per 12.12. Quandoquidem celsitudines basibus reciprocae. Verum per praecedentem. conus cuius basis semidiameter BP, et celsitudo PR fuit aequalis sphaerico segmento ABD. Ergo sphaericum segmentum ABD aequale est et cono, cuius basis semidiameter AP, et celsitudo aggregatum ex EG, GP: quod est unum ex demonstrandis. Accipe reliquum. Quoniam ratio AP ad PG dupla est eius, quae BP ad PG per 8. sex cuius, et dupla est per 2.12. ratio circuli, cuius semidiameter BP ad circulum, cuius semidiameter PG: ideo AP ad PG erit sicut circulus, cuius semidiameter BP ad circulum, cuius semidiameter PG: fuit autem in praemissa, sicut AP ad PG, sic EG, vel EA ad GS: quare per 13.5. sicut EA, AP simul ad PS totum, sic AP ad PG; et ideo sicut circulus, cuius semidiameter BP ad circulum, cuius semidiameter PG: quamobrem duo coni, quorum unius quidem basis semidiameter est [S:79] PG, et celsitudo aggregatum ex AE, AP, alterius autem basis semidiameter est BP, et celsitudo PS sunt ad invicem aequales, per 12.12. quandoquidem reciproca sunt basibus fastigia. Verum ex praecedenti, conus cuius basis semidiameter BP, et celsitudo PS aequalis est sphaerico segmento BGD: ergo sphaericum segmentum BGD aequale est cono, cuius basis semidiameter est PG, et celsitudo aggregatum ex AE AP: quod supererat demonstrandum.

ALITER

Propositam sphaeram ad datam rationem secare.

Sphaerae propositae diameter sit AB, data ratio CD ad DE, oportet sphaeram AB secare, itaut segmentum ad segmentum sit sicut CD ad DE. Ponatur AF dimidium ipsius AB; et sicut est CE ad ED sic sit FA ad AG: quibus intersit media proportionalis AH; ut scilicet FA, AH, AG sint continuae proportionales; et circa axem FB describatur parabola FHLK; itemque circum non coincidentes FB, XB per punctum G incedat hyperbola GL secans parabolen apud L punctum; et compleatur parallelogrammum LMBX, itemque parallelogrammum AGNB; eruntque per 12.2. conicorum elementorum, parallelogramma LB, BG praedicta inter se aequalia. Quare per 15. sex Euclidis, erit sicut AB ad BM, sic LM ad GA.

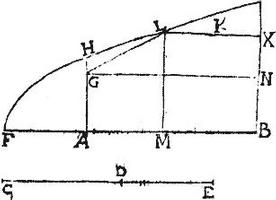
Itaque cum ratio quadrati LM ad quadratum GA, et ideo ratio quadrati AB ad quadratum BM componatur ex rationibus quadrati LM ad quadratum HA, atque quadrati HA ad quadratum AG; et cum ratio FM ad AG componatur ex rationibus MF ad FA, et FA ad AG: cumque per 39. primi conorum elementorum. sit sicut quadratum LM ad quadratum HA, sic MF ad FA; et per 17. sex Euclidis. sicut quadratum HA ad quadratum AG, sic FA ad AG: propterea ex aequa proportione erit sicut quadratum LM ad quadratum AG; et ideo quadratum AB ad quadratum BM, sic MF ad AG: et per 2.12. Euclidis, sic etiam circulus, cuius semidiameter AB ad circulum cuius semidiameter BM; itaque per 12. praedicti, conus, cuius axis AG, basisque semidiameter AB aequalis erit cono, cuius axis FM, basisque semidiameter BM: quandoquidem celsitudines basibus sunt reciprocae: sed per 11.12. Euclidis. sicut conus cuius axis FA, basisque semidiameter AB ad conum, cuius axis GA basisque semidiameter AB, sic FA ad AG: ergo sicut conus, cuius axis FA, basisque; semidiameter AB ad conum, cuius axis FM, basisque semidiameter MB: sic etiam FA ad AG, hoc est CE ad ED. Verum per praecedentem 32. conus, cuius axis FM, basisque semidiameter BM aequalis est sphaerico segmento, cuius axis BM. Item per corollarium 25. huius. conus cuius axis FA, basisque semidiameter AB aequalis est sphaerae, cuius diameter AB. Igitur sicut sphaera AB ad sphaericum segmentum cuius axis BM, sic CE ad ED: et disiunctim sicut CD ad DE, sic sphaericum segmentum, cuius axis AM ad sphaericum segmentum cuius axis BM. Quare sphaera, cuius diameter AB in [S:80] puncto M ipsius diametri secatur in duo segmenta, quorum ratio est, quae CE ad ED. Quod fuit faciendum. Haec propositio sumpta est ex Dionysiodoro mathematico antiquissimo, ut tradit Eutocius Ascalonita in commentariis Archimedis.