PROPOSITIO XXXI.

Idem aliter ostendere.

Sunto datae rectae AB, BG in rectum positae, describatur circa axem AG parabole ADH, quam in puncto D secet recta BD ipsi AG perpendicularis; et per punctum D ipsi AG parallelus agatur EDZ, cui a punctis A, G lineae ipsi BD parallelae occurrant ad puncta E, Z lineae AE, GZ; item per punctum Z circa non coincidentes EA, AG describatur hyperbole ZH, quae secet parabolam in puncto H, a quo ad lineas AE, AG perpendiculares cadant lineae HT, HK; et per sextam huius, ipsis AB, AT media proportionalis intersit AL.

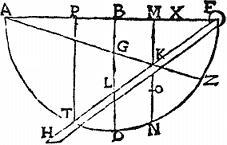
Aio itaque quod AL, AT mediae proportionales interiacent ipsis AB, AG. Nam cum hyperbole sit HZ, non coincidentes autem KAG, iam per 12. secundi Conicorum Elementorum, rectangulum AH aequale erit rectangulo AZ: quare per 15. sexti Elementorum Euclidis erit sicut AT ad AG, sic GZ hoc est BD ad TH; sed per 20. primi Conicorum Elementorum ratio AB ad AT dupla est rationis BD ad TH, quandoquidem parabole est ADH: ergo, et ratio AB ad AT dupla est rationis AT ad AG: quare fiet sicut AB ad AL, vel sicut AL ad AT (eadem enim ratio per hypothesim) sic AT ad AG. Igitur AB, AL, AT, AG continuae proportionales sunt. Quod fuit demonstrandum. Et haec est inventio Menaechmi aliis modis commendatior, quoniam innititur geometricis, et absolubilibus praeceptis, quando aliis fortuito casu videantur quodammodo intentum adipisci. Sed huic adde, quod si [S:18] AB, BD ponantur aequales, et mox per AD puncta parabole ADH describatur, et reliqua, ut prius, erit per iam demonstrata sicut BD, hoc est AB ad TH, sic AT ad AG, sed per 20. primi Conicorum ratio AB ad AT dupla est rationis ipsius BD, hoc est, AB ad TH: igitur hac via fient AB, TH, AT, AG continue proportionales: nec opus est ipsius AL interpositione, quemadmodum Menaechmus docet.