F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Praeparatio ad Archimedis opera 30
<- App. -> <- = ->

PROPOSITIO XXX.

Aliter illud idem demonstrare.

Sint datae rectae lineae AB, et CD, et intra parallelogrammata rectangula inter se aequalia, et similia, quorum maiora latera aequalia sint AB maiori datarum; [S:17] disponendaque sunt parallelogrammata in eodem plano, ut eorum bases minores super eadem recta BK iaceant, et eorum diametri, aequidistent inter se, et fixo manente parallelogrammo medio compellatur unum supra, alterum infra eundem, aptata in eodem plano; quousque puncta A, E, H extrema diametrorum, in una recta linea AK cadant; quae praeterea cum recta BK, extremi parallelogrammi lateris portionem CD abscindat aequalem minori datarum.

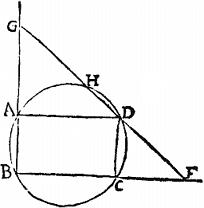
figura 20

Hoc enim facto ipsae EF, GH mediae proportionales erunt inter ipsas AB, CD: nam propter triangulorum similitudinem, sicut AB ad EF, sic AK ad KE; sicut autem AK ad KE, sic FK ad KG; sed et FK ad KG, sicut EF ad HG. Igitur sicut EF ad HG, sic AB ad EF: rursum, sicut EF ad HG, sic EK ad KH; sicut autem EK ad KH, sic GK ad KC; sed et GK ad KC, sicut HG ad CD. Igitur EF ad HG, sicut HG ad CD. Constat ergo lineas AB, EF, HG, CD esse in proportione continua, sicut fuit demonstrandum. Et haec est Eratosthenis traditio.

Inizio della pagina
 ->