PROPOSITIO VIII.
Circulorum peripheriae sunt diametris proportionales.
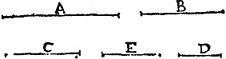
Sint circuli AIB, et CKD quorum diametri AB, CD; sitque sicut peripheria AIB ad periferiam CKD sic diameter AB ad lineam EF, per quintam huius. Et demonstrandum erit, quod linea EF aequalis erit lineae CD. Nam si linea EF maior est, quam linea CD: intelligatur circulus ELF concentricus circulo CKD, et inscribatur circulo ELF figura multiangula ENF minime tangens circulum CKD, per [S:6] decimamtertiam duodecimi Elementorum Euclidis. Et ei similis figura AMB inscribatur circulo AIB, eritque sicut linea AB ad lineam EF, sic perimeter figurae AMB ad perimetrum figurae ENF, et ideo sicut peripheria AIB ad peripheriam CKD, et permutatim sicut perimeter AMB ad peripheriam AIB, sic perimeter ENF ad peripheriam CKD: sed per secundum postulatum maior peripheria AIB perimetro AMB, igitur, et maior peripheria CKD, perimetro ENF; inclusa videlicet maior includente: quod est contra dictum postulatum. Non est ergo maior linea EF, quam linea CD. Si autem minor, tunc conversim erit, sicut peripheria CKD, ad peripheriam AIB, sic iam linea EF ad lineam AB. Sit itaque sicut linea EF, ad lineam AB, sic linea CD, ad lineam GH, per quintam huius. Eritque sicut linea CD, ad lineam GH, sic peripheria CKD ad peripheriam AIB; et erit per 14. quinti, quoniam CD maior, quam EF, iam, et GH maior, quam AB. Unde sequitur idem impossibile, quod prius, ut scilicet peripheriae primae ad peripheriam secundam ratio sit, sicut prima diameter ad lineam maiorem secunda diametro. Non est igitur linea EF minor, quam linea CD. Sed nec maior fuit. Aequalis erit ergo. Quod fuit demonstrandum.