PROPOSITIO XVI.

Omnis portio conoidis hyperbolici solidi plano ad axem recto abscissa ad conum eamdem basim, eumdemque axem cum portione habentem, et sicut linea, quae constat ex axe portionis, et ex tripla axi adiectae ad lineam, quae constat ex eodem axe, et ex dupla eiusdem adiectae.

Esto portio conoidis solidi hyperbolici ABC, cuius axis BD, quod sectum plano per axem faciat hyperbolen ABC per 16. praecedentis; cuius plani cum plano ad axem recto, et portionem abscindente communis sectio sit recta AC; eritque per 17. praemissi sectio in solido per planum abscindens facta circulus, cuius diameter AC; super quem circulum conus constituatur habens verticem B, axemque BD: item BE in hyperbole sit linea axi adiecta, eique aequales singulae sunto EF, FG. Erit autem E centrum hyperboles, et BF eius transversa diameter. Demonstrandum est igitur, quod portio conoides ABC ad conum ABC est sicut linea GD ad lineam DF. Ponatur conus Z ad conum ABC sicut linea GD ad lineam DF: et ostendendum erit, quod portio ABC aequalis est cono Z. Sit BH tertia pars ipsius BD: et linea GD erit tripla ipsius EH: ponatur cylindrus super circulum AC, axemque BD, quod sit ABC, qui per 15. praecedentis triplus erit coni ABC; et ideo cylindrus ABC ad conum ABC, sicut linea GD ad lineam EH; cumque conus ABC ad conum Z sit sicut DF ad lineam GD; erit iam ex aequali perturbataque proportione cylindrus ABC ad conum Z, sicut linea DF ad lineam EH: itaque si portio ABC non sit aequalis cono Z, esto [S:259] si possibile est, portio maior cono, aliquo excessu: fiatque per 8. huius, et corollarium 9. figura inscripta portioni, ita ut portio addat super figuram inscriptam minus dicto excessu: idque fiat secto axe BD, cylindroque ABC, quot in partes opus fuerit, ut puta in quinque BI, IK, KL, LM, MD. Exponantur totidem rectangula sub eadem altitudine lineae FB basibus vero BD, BM, BL, BK, BI; quae rectangula sint N, O, P, Q, R, quibus applicentur singulis quadrata ex singulis dictis basibus facta S, T, V, X, Y.

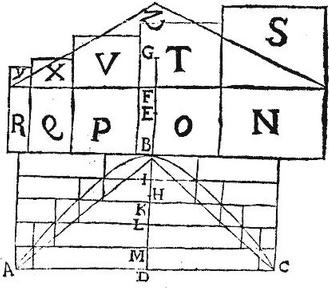
Unde spatium NS erit ipsum rectangulum FDB, spatium OT ipsum rectangulum FMB, spatium PV ipsum rectangulum FLB, spatium QX ipsum rectangulum FKB, spatium RY ipsum rectangulum FIB. Itaque cum linea DF sit altitudo maximi spatii NS, atque linea EH constet ex BH, quae est tertia pars ipsius BD, quod est latus quadrati S, et ex EB, quae est semissis ipsius FB, quae est altitudo spatii N: ideo per 3. precedentis, quintuplum spatii NS ad aggregatum quatuor spatiorum OT, PV, QX, RY maiorem rationem habet, quam linea DF ad lineam EH: et ideo maiorem quam cylindrus ABC ad conum Z: quoniam vero quinque cylindri in quos secatur cylindrus ABC, quorum basium semidiameter est DA: item quatuor cylindri componentes figuram portioni inscriptam, quorum basium semidiametri sunt reliquae quatuor ordinatae a punctis L, M, K, I, ad peripheriam hyperboles receptae; singuli inquam hi quatuor, et AMC cylindri sunt eiusdem altitudinis, quae est quinta pars lineae BD: ideo per 15. praemissi tales cylindri sunt basibus proportionales; bases autem per 2. duodecimi Euclidis sunt quadratis semidiametrorum DA, et quatuor reliquarum ordinatarum proportionales: quadrata vero huiusmodi per 21. primi conicorum elementorum sunt spatiis NS, OT, PV, QX, RY proportionalia. Unde ex 2. praemissi sequitur, ut quintuplum cylindri AMC, hoc est totalis cylindrus ABC ad aggregatum quatuor cylindrorum componentium figuram portioni inscriptam sit sicut quintuplum spatii NS ad aggregatum quatuor spatiorum OT, PV, QX, RY: sed quintuplum dicti spatii ad aggregatum dictorum quatuor spatiorum maiorem rationem habuit, quam cylindrus ABC ad conum Z. Ergo et cylindri ABC ad figuram inscriptam ratio maior erit, quam eiusdem cylindri ABC ad conum Z; quare figura inscripta minor erit cono Z: fuerat vero maior, quod est absurdum. Non est ergo portio ABC maior cono Z. Sit autem post haec minor: et tunc per eadem, quae prius, fiat figura circumscripta portioni ABC; itaut excessus, quo superatur portio a figura circumscripta sit minor, eo quo portio superatur a cono Z; et perinde conus Z sit maior figura circumscripta: tunc autem rursus per 3. praemissi quintuplum spatii NS ad aggregatum omnium [S:260] quinque spatiorum NS, OT, PV, QX, RY minorem rationem habebit, quam linea DF ad lineam EH, hoc est quam cylindrus ABC ad conum Z.

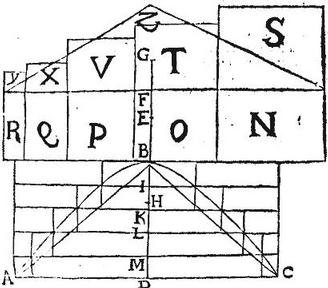
Per eadem, quae prius, quintuplum cylindri ABC, hoc est totus cylindrus ABC ad aggregatum quinque cylindrorum componentium figuram circumscriptam, erit sicut quintuplum spatii NS ad aggregatum quinque spatiorum NS, OT, PV, QX, RY. Sed quintuplum dicti spatii ad aggregatum quinque dictorum spatiorum minorem rationem habuit, quam cylindrus ABC ad conum Z. Ergo et ratio cylindri ABC ad figuram circumscriptam minor erit, quam ratio eiusdem cylindri ABC ad conum Z. Quare figura circumscripta maior erit cono Z: fuerat autem minor, quod est absurdum. Non est ergo portio ABC minor cono Z; sed nec maior potuit esse: aequalis ergo erit portio ABC cono Z. Quod fuit demonstrandum.