PROPOSITIO XVII.

Quod si portio hyperbolici solidi plano ad axem obliquo abscindatur; similiter ad conum eiusdem basis, axisque dictarum quoque linearum rationem habere probatur: qui tamen conus, quoniam pro basi ellipsi habet, segmentum esse alicuius coni circularem basim habentis ostensum est.

Eadem, huic descriptio, idemque processus inserviet, qui praecedenti: hoc tamen excepto, quod hic plana solidum secantia obliqua sunt ad axem: atque ideo per 24. praemissi portio ipsa solidi, cylindrus totalis, conusque ellipses pro basibus habebunt; et per corollarium praedictae reliqui cylindri pro basibus ellipses praedictae similes habebunt: verum pe 11. et per 13. praecedentis tales cylindri sunt frusta cylindrorum circulares bases habentium: et talis conus frustum est alicuius coni circularem basem habentis; cumque per 14. et 15. praecedentis, talia cylindrorum frusta sint basibus proportionalia propter aequales axes, et cylindrus talis ad conum eiusdem basis, et axis sit triplus. Iam iisdem mediis, quibus in praemissa demonstrabimus, et in hac, quod portio ABC non maior, nec minor, sed aequalis est cono Z, qui ad conum ABC ponitur sicut linea GD ad lineam DF; quod iam, et in praemissa, et hic proponitur demonstrandum. [S:261]

SCHOLIUM I.

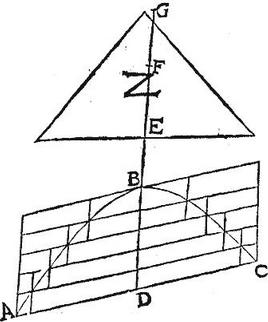
Oportet autem ut BD hyperboles ABC diameter semper transeat per E centrum sectionis, quo secet diametros cylindrorum basis singulas per aequalia per 47. primi conicorum ut in 9. huius traditum est in formatione figurae tam inscriptae, quam circumscriptae.

SCHOLIUM II.

Notandum etiam, quod sicut in duabus praemissis axis BD secatur in quinque partes aequales, et cylindrus ABC in totidem cylindros aequales: sic cum secandus erit tam axis, quam cylindrus in plures partes, ut cumque ad demonstrationem opus fuerit, agendum erit in demonstratione per numerum partium assumptum; ut scilicet totidem sint, et cylindri constituentes figuram circumscriptam; qui vero componunt figuram inscriptam sint semper unitate pauciores.