F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis de conoidibus et sphaeroidibus figuris Liber secundus 15
<- App. -> <- = ->

PROPOSITIO XV.

Portiones de conoide paraboles utcumque planis abscissae, sunt adinvicem sicut axium quadrata.

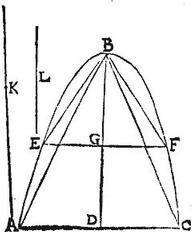
figura 11

Esto conoides solidum a parabola ABC circum axem BD circumlata descriptum, de quo abscindantur planis utcumque ductis duae portiones, quarum axes K, L. Aio quod portio, cuius axis K ad portionem cuius axis L est sicut quadratum K ad quadratum L: capiantur enim de axe solidi ipsa quidem BD ipsi K aequalis; ipsa vero BG ipsi L aequalis ductisque per puncta D, G planis ad [S:258] axem rectis duae de solido portiones abscindantur ABC, EBF: eritque per antepraemissam, portio cuius axis K aequalis portioni ABC, quando aequales axes habent: portio quoque, cuius axis L aequalis portioni EBF, quando aequales etiam sortiuntur axes.

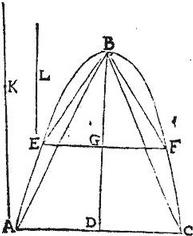
figura 12

Itaque demonstrandum est, quod portio ABC ad portionem EBF, est sicut quadratum BD, ad quadratum BG; hoc modo. Plana per D, G ducta, quoniam recta sunt ad axem, faciunt in solidocirculos per 17. praemissi, quorum diametri AC, EF; intelligantur ergo super tales circulos coni, communes axes BD, BG; eumdemque verticem B cum portionibus habentes. Quia conus ABC ad conum EBF proportionem compositam habet ex ratione basis circularis AC ad basim EF, seu quadrati AD ad quadratum EG, et ex ratione altitudinis DB ad altitudinem GB; sed ex 20. libri primi conicorum quadratum AD ad quadratum EG est sicut DB ad GB: ergo conus ABC ad conum EBF duplam proportionem habet altitudinis DB ad altitudinem GB, seu eandem quam habet quadratum DB ad quadratum GB: sunt vero ex 10. huius portiones conoidales sexquialterae conorum comprehensorum. Igitur conoidis portio ABC ad portionem EBF est sicut quadratum DG ad quadratum GB. Quod erat demonstrandum.

Inizio della pagina
 ->