|
| F r a n c i s c i M a u r o l y c i O p e r a M a t h e m a t i c a |
Exemple de source Mauro-TeXJean-Pierre Sutto |
màj 10 jan. 2001 |
1. Source Mauro-TeX
Le texte qui suit est un extrait du fichier source Mauro-TeX de la transcription d'une proposition d'un texte mathématique ayant deux témoins, accompagné de sa sortie postscript (pour impression, convertie en jpeg pour l'occasion) et sa sortie html pour l'édition internet édition internet.
Le fichier source Mauro-TeX est tel qu'il apparaît dans un bon éditeur de texte sachant colorer automatiquement les balises LATEX et leurs arguments. Précisons que les retours à la ligne et les lignes commençant par un % ne sont pas significatifs dans le Mauro-TeX, ce qui permet de présenter le texte de la façon la plus agréable lors des travaux de transcription et d'édition.
| source Mauro-TeX |
|
\Prop{A.I-54} |
2. Postscript (converti en jpeg)
Après l'action du préprocesseur
LATEX aidé des macros
Mauro-TeX et l'insertion des éventuelles figures, le texte
imprimé a l'allure suivante (le postscript a été
converti à la résolution d'un écran standard):
| postscript converti en jpeg |

|
Le résultat pour l'édition internet qui suit, ne rend pas
compte des liens entre propositions, apparat critique et notes. Voir
une proposition complète et son environnement (par exemple celle
correspondante à l'extrait) pour avoir la possibilité
d'activer des « frames » et visualiser
commodément l'apparat critique, variantes et notes
éditoriales. Voir aussi l'aide pour
des informations sur la navigation dans les pages de ce site.
| web html |
|
54a Duabus datis lineis terminatis ad rectos invicem; invenire circa diametrum alteram ipsarum coni sectionem vocatam ellipsin1, in eodem plano lineis2, cuius summitas sit punctum, quod est ad rectum angulum applicatae autem a sectione ad diametrum in dato angulo possint id, quod adiacentia rectangula ad alteram lineam3, latitudinem habentia receptam sub ipsa ad summitatem sectionis, deficientia specie simili et similiter posito4 contento sub datis lineis. Sint ad rectos datae ba ag quarum maior ab. \\ Datusque angulus primum5 rectus. \\ Oportet in subiecto plano bag ellipsim describere: cuius diameter sit ab. \\ Summitas a. \\ Recta diametros ag. \\ Et ordinatae6 ad datum angulum applicatae. Exurgat ex ab planum rectum ad subiectum, in quo circuli peripheria adb describatur bifariam secta apud d. Et coniungantur ad db7. Sitque ipsi ag aequalis ax. Et penes ipsam db agatur xo8. Et penes ipsam ab agatur oz. 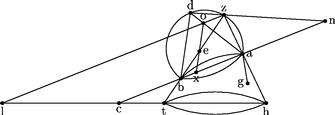
\\ Et coniungantur az zb et producantur. Et a puncto utcunque9 relicto in za quod sit h agatur penes de linea ht coincidens ipsi ab apud c ipsique zo apud l. \\ Eritque, per 26am tertii Euclidis angulus abd10 aequalis angulo dzb. |
1 ellipsin A ellipsim S |