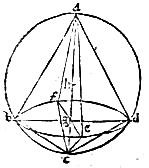
PROPOSITIO XVI
127 Omnes circuli maiores in sphaera dividunt se invicem per aequalia.
128 Sunto duo circuli maiores abc adc in sphaera, cuius centrum e, designati: aio quod horum uterque secat reliquum per aequalia. 129 Nam per 7 huius, horum uterque circulorum transit per centrum sphaerae atque ideo, ex prima parte corollarii primae huius, e centrum sphaerae erit centrum commune circulorum abc adc. 130 Igitur e centrum erit in communi sectione planorum circulorum, quae per 3 undecimi linea recta est. 131 Sit ergo communis sectio circulorum abc adc recta ac: in recta itaque ac erit centrum ipsorum e; igitur ac recta diameter est tam circuli abc quam circuli adc; quam ob rem ipsi arcus abc adc semicirculi sunt et residui semicirculi, quod erat demonstrandum.