PROPOSITIO XXXII

233 In triangulo rectangulo ex arcubus magnis in superficie sphaerae constituto, sinus totus ad sinum arcus unum ex acutis angulis⁴⁸ subtendentis est sicut umbra versa reliquo acuto angulo debita ad umbram versam lateris dictum acutum respicientis.

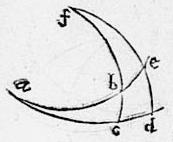
234 Hoc est in eadem descriptione ostendam quod: sinus totus, scilicet arcus da, ad sinum arcus ac est sicut umbra versa arcus de ad umbram versam arcus bc. 235 Per ultimum corollarium 30 praecedentis, ex umbra versa arcus de in versam arcus fe sui complementi producitur quadratum gnomonis. 236 Sed per praecedentem, quadratum gnomonis ad rectangulum umbrarum versarum arcuum fe bc fuit sicut sinus arcus da ad sinum arcus ac. 237 Igitur et sicut quod fit ex umbra versa arcus de in umbram versam arcus fe ad rectangulum⁴⁹, quod fit ex umbris versis arcuum fe bc sic sinus arcus da scilicet sinus totus ad sinum arcus ac. 238 Cumque per primam sexti Euclidis, rectangulum umbrarum versarum arcuum de fe ad rectangulum umbrarum versarum arcuum fe bc sit sicut umbra versa⁵⁰ arcus de ad umbram⁵¹ versam arcus bc. Erit iam sicut sinus totus ad sinum arcus ac sic umbra⁵² versa arcus de ad umbram versam⁵³ arcus bc. Quod fuit demonstrandum. 239 Et eadem omnia concludere potes de rectis umbris, quae talium arcuum complementis debentur.

SCHOLIUM

240 Ex his igitur demonstrationibus absolvi possunt omnes questiones, quae fieri consueverunt circa sphaeralia triangula: quaeque in astronomia pertinent ad arcus circulorum in primo coelo intellectorum, hoc est in concava superficie primi mobilis descriptorum. 241 Sed nemo harum speculationum scientiam perfectam habens nesciet theoriam ad praxim atque demonstrationem ad calculum deducere. 242 Quae res ut magis pervia fiat lectori exempla nonnulla sunt adducenda, ut circa declinationes et ascensiones.

243 Et primum si in descriptione praecedentis circulus acd sit aequator, circulus abe sit zodiacus, circulus fed sit colurus incedens per utrosque eorum polos, punctum a punctum aequinoctii, arcus de maxima zodiaci⁵⁴ declinatio, punctum b locus astri in zodiaco, circulus fbc circulus declinationis, arcus bc declinatio astri. 244 Ex loco autem astri cognito et maxima declinatione data, hoc est ex arcubus ab de quaeratur declinatio astri, hoc est arcus bc. 245 Absolvetur questio sic cum per 6^m praemissi libri, sicut est sinus totus ad sinum arcus de sic sit sinus arcus ab ad sinum arcus bc. 246 Atque ex his quatuor, tria cognita sint: noscetur et reliquum, per regulam quatuor magnitudinum. 247 Hoc est, cum sinus totus datus sit sinusque arcus de dati datus, nec non sinus arcus ab dati, propter cognitum astri locum, datus. Iam et reliquus sinus arcus bc quaesiti dabitur et perinde arcus bc quaesitus dabitur. 248 Unde si ducatur secundum in tertium et productum dividatur in primum, exibit ex divisione 4^m ex doctrina 14 sexti Elementorum Euclidis. Hoc est, si ducatur sinus arcus de in sinum arcus ab et productum dividatur in sinum totum, exibit ex divisione sinus arcus bc, unde et arcus bc quaesitus notus erit.

249 Si autem sumatur arcus fbc pro horizonte recto, erit arcus ac ascensio recta respondens arcui zodiaci ab. 250 Itaque quoniam per 17^m praecedentis libri, sinus secundus arcus bc ad sinum secundum arcus ab est sicut sinus totus ad sinum secundum arcus ac, hoc est sinus arcus fb ad sinum arcus be sicut sinus totus ad sinum arcus cd. 251 Atque ex his tria nota sint, scilicet sinus arcus fb sinus arcus be sinusque totus, iam et reliquum scilicet sinus [S:59v] arcus cd noscetur. Unde et arcus cd dabitur, qui ablatus a quadrante relinquit arcum ac ascensionem scilicet rectam cognitam. 252 Similiter et caeterae quaestiones absolventur, quae faciles erunt horum libellorum theoremata intelligentibus. 253 Lubet tamen hic demonstrare praxim, qua Ioannes Regiomontanus utitur in calculanda declinatione et ascensione recta per tabulas generales, nec non in habenda differentia ascensionali. Non enim apertum est omnibus ingeniis unde pendeant illius calculi regulae.

254 Itaque pro tabula declinationum sit zodiacus ab, aequator ac, locus longitudinis astri in zodiaco punctum b, latitudo astri bg ita ut punctum g sit versus astri locus, declinatio arcus gh. 255 Producatur arcus gb usque ad aequatorem ad punctum c, iam intranti in tabulam declinationum generalem cum longitudine astri occurrit primum arcus bc qui arcus est circuli latitudinis astri inter zodiacum et aequatorem compraehensus. 256 Ex quo quidem arcu et latitudine astri bg sive aggregando sive subtrahendo, notus veniet arcus gc arcus videlicet circuli latitudinis inter centrum astri et aequatorem. 257 Deinde occurrit in tabula numerus multiplicandus, qui numerus est sinus rectus anguli gch posito sinu toto partium 100000. Unde apud punctum tropicum, quoniam talis angulus rectus est, ponitur numerus ipse sinus totius, quandoquidem anguli recti sinus est sinus totus. 258 Per 6^m autem praecedentis libri, sinus totus ad sinum anguli gch est sicut sinus arcus cg ad sinum arcus gh. 259 Quorum cum tria nota sunt scilicet sinus totus 100000 sinus anguli gch, qui est 260 numerus⁵⁵ multiplicandus tabulae ac sinus arcus cg iam per regulam quatuor magnitudinum noscetur et reliquum, scilicet sinus arcus gh. 261 Recte⁵⁶ igitur praecipit Ioannes in problemate, dum iubet multiplicari sinum arcus gc in numerum multiplicandum in tabula repertum, hoc est multiplicari 2^m in 3^m et productum dividi per primum, hoc est per sinum totum 100000. 262 Talis enim divisio fit dum in numero ex multiplicatione producto abiiciuntur quinque ad dextram figurae quot sunt zifrae in divisore, hoc est in sinu⁵⁷ toto, quae operatio notissima est arithmeticis. 263 Additur autem relictarum figurarum numero unitas, si figurae abiectae denotant plusque 50000, quoniam fractio, quae ultra integras partes, ex divisione exit, minor est dimidio, cum abiectae figurae minus quam 50000 hoc est minus quam dimidium divisoris denotant et tunc negligitur. 264 Maior autem est dimidio, cum relictae figurae plus dicto dimidio denotant et tunc pro fractione integra unitas adiicitur, hoc est integra pars. 265 Talis ergo numerus ex divisione sic facta progrediens, erit quartum quod quaerebatur, hoc est sinus ipsius arcus gh, hoc est declinationis quaesitae: unde ex tabula sinus recti declinatio ipsa cognita venit. 266 Nec interest utrum sinus arcuum cg gh capiantur respectu alterius sinus totius, quam sinus anguli gch qui capitur respectu sinus totius partium 100000 quandoquidem in quatuor magnitudinibus proportionalibus, non necesse est omnes quatuor esse eiusdem colligantiae, sed primam cum secunda et tertiam cum quarta.

267 Pro tabula autem ascensionum rectarum, repeto descriptionem ultimae propositionis huius libri, in qua quidem aequator sit acd, circulus latitudinis astri abe, circulus declinationis eiusdem fbc, circulus autem fed incedens per polos ipsorum abe acd determinet ae ad quadrantes, punctum b centrum astri, arcus bc declinatio astri, arcus ac differentia transitus astri per coeli medium. Itaque intranti tabulam ascensionum generalem cum longitudine astri occurrit primum arcus, qui inscribitur radix ascensionum, qui quidem est arcus aequatoris ab initio Arietis secundum ordinem signorum usque ad circulum latitudinis astri abe computatus. 268 Deinde occurrit numerus multiplicandus, qui nihil aliud est quam umbra versa arcus fe multiplicata in senarium, posito gnomone partium 100000. 269 Et quoniam per 31^m huius praecedentem, sinus totus ad sinum arcus ac est sicut quadratum gnomonis ad quadrangulum quod fit ex umbris versis arcuum fe bc. 270 Iam, si dictum quadrangulum ducatur in sinum totum et productum dividatur in quadratum gnomonis, exibit ex divisione sinus arcus ac. 271 Sed cum sinus totus hic supponatur partium 60000 et numerus multiplicandus in tabula inventus sit umbra versa arcus fe ducta in 6. Atque quadratum gnomonis sit 10000000000 in idem redit operatio, si ducatur numerus multiplicandus in umbram versam arcus bc declinationis et a producto abiiciantur sex figurae, quandoquidem canon iubet abiici quinque figuras, ob id videlicet, quod numero multiplicando ablata sit una figura ad alleviandum laborem. 272 Et si abiectae denotent plusque est 50000 adiicienda relicto numero unitas ob causam superius memoratam. Hoc pacto relictus numerus est is, qui ex divisione proditurus erat: hoc est sinus arcus ac, unde et ipse arcus ac notus fiet. 273 Cumque radix ascensionum per tabulam cognita sit arcus aequatoris a puncto aequinoctiali verno usque ad punctum a computatus, iam addito vel ablato arcu ac nunc noto, cognitus veniet arcus aequatoris ab eodem aequi[S:60r]noctii puncto usque ad punctum c computatus, hoc est ascensio astri recta quaesita, quae a circulo declinationis fbc determinatur. 274 Verum ipse arcus ac differentia scilicet transitus astri per coeli medium potest absque auxilio numeri multiplicandi et absque tabula umbrarum haberi sic.

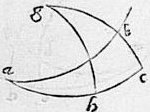
275 In descriptione praemissa, per tabulam declinationum notus erat arcus cg latitudinis astri inter aequatorem ac et centrum astri g comprehensus. Notus item fuit arcus gh declinatio scilicet astri atque ideo sinus secundi horum arcuum cogniti fient. 276 Verum per 17^m praemissi libri, sinus secundus arcus gh ad sinum secundum arcus gc est sicut sinus totus ad sinum secundum arcus ch quandoquidem rectus est angulus ghc. 277 Igitur cum ex his tria nota sint, noscetur et reliquum, scilicet sinus secundus arcus ch. Et perinde ipse arcus ch qui quaerebatur, notus erit, differentia scilicet transitus astri per coeli medium: unum, ut prius, per radicem ascensionum, data fiet ascensio recta quaesita. 278 Unde pro ascensione recta satis erat radix ascensionum sola absque numero multiplicando et absque usu tabulae Foecundae, quae tabula est umbrarum. 279 Ioannes autem vir perspicacissimus ideo adiecit numerum multiplicandum, usumque tabulae Foecundae, ut caveret divisionem, quae necessaria est ei, qui per solam radicem ascensionum operatur, quae divisio, cum scilicet divisor numerus diversas habet figuras, fastidiosior est numeranti: sic invenit modum, qui sola multiplicatione perficeretur, quae calculatoribus notior esse consuevit.

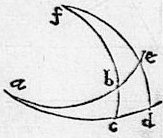
280 Pro regula tandem inveniendi ascensionalem differentiam, sit rursum in descriptione 31 praecedentis, aequator acd, horizon rectus fbc obliquus abe, meridianus fed, eritque latitudo regionis arcus fe, centrum astri punctum b, declinatio astri arcus bc, differentia ascensionalis eius arcus ea. 281 Et quoniam per 31^m praecedentem, quadratum⁵⁸ gnomonis ad quadrangulum factum ex umbris versis arcuum fe bc hoc est latitudinis loci et declinationis astri, est sicut sinus totus ad sinum arcus ac atque ex his quatuor tria nota sint scilicet quadratum gnomonis quadrangulum ex umbris factum et sinus totus, ideo reliquum scilicet sinus arcus ac notus veniet: recte⁵⁹ igitur praecipit Ioannes multiplicari umbras versas latitudinis loci ac declinationis astri alteram in alteram, inde enim quadrangulum praedictum produci; tale enim quadrangulum in sinum totum, quem ipse supponit partium 60000 multiplicatum ac in quadratum gnomonis hoc est in 10000000000 divisum exhibet sinum arcus ac. 282 Id autem fit, dum praedictum quadrangulum in senarium ducitur et a producto sex ad dextram figurae⁶⁰ abiiciuntur relicto unitate⁶¹ adiecta, si abiectae plusquam 50000 denotaverint. 283 Nam talis relictus numerus erit sinus arcus ac. Quare notescet arcus ac quae differentia ascensionum quaesita est.

284 Sic iam demonstrata est praxis dictarum Tabularum ac simul declaratum est, qua ratione constructae sint.