PROPOSITIO XXIII

168 Si fuerint duo triangula in superficie sphaerae ex arcubus circulorum maiorum [S:57v] quorum unius acutus angulus aequalis alterius acuto angulo et sinus arcuum acutis oppositorum proportionales sinibus arcuum duos ex reliquis angulos respicientium: tunc hi anguli aut aequales erunt aut coniuncti duos rectos conficient.

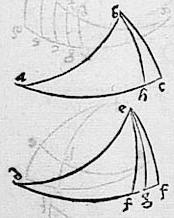
169 Sint in superficie sphaerae duo triangula abc def ex arcubus circulorum maiorum in quibus anguli a d acuti sint invicem aequales et sicut est sinus arcus ab ad sinum arcus de sic sit sinus arcus bc ad sinum arcus ef: aio tunc quod angulus c aut aequalis erit angulo efd aut cum eo iunctus conflabit duos rectos. 170 Nam si rectus sit angulus c, rectus erit et angulus f. 171 Si enim existente c angulo recto, rectus non sit f angulus, non erit arcus ef perpendicularis ad arcum df. 172 Ducatur ergo perpendicularis arcus circuli maioris eg ad arcum df et tunc, quoniam aequales sunt anguli a d atque recti qui ad c g anguli, iam per 7^m praecedentis libri, erit sinus arcus ab ad sinum arcus bc sicut sinus arcus de ad sinum arcus eg. 173 Sicut per hypothesim et conversam proportionem, sinus arcus ab ad sinum arcus bc sicut sinus arcus de ad sinum arcus ef, igitur quam habet rationem sinus arcus de ad sinum arcus ef eam habet et ad sinum arcus eg. Aequales ergo sunt sinus arcuum fe eg et perinde ipsi arcus fe eg aequales erunt. Quod est impossibile. 174 Omnino igitur existente angulo c recto, rectus erit et f angulus, et ob id in eo casu aequales erunt c f anguli. Hinc sequitur ut si rectus non sit c angulus, neque rectus iam esse possit efd angulus. 175 Tunc ergo ducantur circulorum maiorum arcus eg bh perpendiculares ad ipsos df ac arcus, qui quidem perpendiculares aut ambo cadunt intra abc def triangula, aut unus intus, alter extra. 176 Cadant primum ambo intus. Et tunc quoniam per hypothesim et conversam proportionem, sinus arcus bc ad sinum arcus ba sicut sinus arcus fe ad sinum arcus ed et per 7^m praemissi, sinus arcus ab ad sinum arcus bh sicut sinus arcus de ad sinum arcus eg. Propterea ex aequali, sinus arcus cb ad sinum arcus bh erit sicut sinus arcus fe ad sinum arcus eg. 177 Quare per 8^m praecedentis, quoniam recti sunt, qui ad g h anguli, aequales erunt c f anguli sicut prius. 178 Cadant deinde perpendiculares arcus eg bh alter intus, alter extra: hoc est bh intra triangulum⁴⁰ abc et arcus eg extra: dico tunc quod angulus c cum angulo efd iunctus duos rectos faciet. Quod sic ostendam. 179 Rursus enim per hypothesim et conversim, sinus arcus bc ad sinum arcus ba sicut sinus arcus fe ad sinum arcus ed et per 7^m praemissi, sinus arcus ab ad sinum arcus bh sicut sinus arcus bh⁴¹ sicut sinusarcus de ad sinum arcus eg et rursus ex aequali, erit sinus arcus cb ad sinum arcus bh sicut sinus arcus fe ad sinum arcus eg. 180 Quare et ut prius, per 8^m praemissi, aequalis erit angulus c angulo efg. Sed angulus efg cum angulo efd conflat duos rectos, ergo et angulus c cum angulo efd conficiet duos rectos. Quod erat demonstrandum. Itaque constat, quidquid proponitur demonstrandum.