PROPOSITIO XXXV

209 Iisdem suppositis si sinus totus ad sinum secundum alterius perpendicularium arcuum fuerit sicut sinus secundus reliqui perpendicularis ad sinum secundum anguli acuti praedicti: tunc arcus inter casus perpendicularium aequalis erit arcui inter puncta signata cadenti; reliquae autem coalternae quadrantum portiones aequales erunt; et angulorum a perpendicularibus arcubus⁴³ apud signata puncta factorum sinus erunt aequales alter alterius perpendicularis sinui secundo.

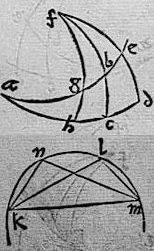
210 In eadem descriptione ponatur sicut sinus totus ad sinum arcus fg sic iam sinus arcus fb ad sinum arcus fe: aio quod tunc arcus ch aequalis erit arcui bg. 211 Nam propter proportionem sinuum, per15^m sexti Euclidis, quadrangulum ex sinu toto sinuque arcus fe⁴⁴ aequale erit quadrangulo ex sinibus arcuum fg fb. Sed per praecedentem, sicut illud quadrangulum ad hoc quadrangulum sic sinus arcus hc ad sinum arcus bg igitur sinus ille, huic aequalis⁴⁵ erit, quare arcus ipsi ch bg aequales erunt. Quod est propositum. 212 Item aio quod arcus ag arcui cd aequalis erit et arcus ah aequalis arcui be. Nam per 7^m huius, sinus arcus ga ad sinum arcus ah est sicut sinus arcus gf ad sinum arcus fe. Et per 6^m, sinus arcus cd ad sinum arcus be sicut sinus arcus cf hoc est sinus totus ad sinum arcus fb. 213 Sed per hypothesim, sinus⁴⁶ totus ad sinum arcus fb sicut sinus arcus gf ad sinum arcus fe. 214 Igitur sinus arcus ga ad sinum arcus ah sicut sinus arcus cd ad sinum arcus be. Et ideo chorda dupli arcus ga ad chordam dupli arcus ah sicut chorda dupli arcus cd ad chordam dupli arcus be et quoniam aequales fuerunt arcus ch bg, ideo aggregatum ex arcubus ag be aequale erit aggregato arcuum ah cd, quare aggregatum ex duplis illorum aequale aggregato ex duplis horum. 215 Sit tale aggregatum arcus klm in quo chorda dupli arcus ag sit recta kl et chorda dupli arcus be sit recta lm. Item chorda dupli arcus cd sit recta mn et chorda dupli arcus ah sit recta nk. Et coniungatur recta km. 216 Itaque quoniam fuit chorda kl ad chordam kn sicut chorda mn ad chordam lm et anguli klm mnk aequales, quandoquidem in eandem circuli⁴⁷ portionem cadunt. 217 Propterea per 14^m sexti Euclidis, triangula klm mnk sunt aequalia: sicut super eandem basim km constituta sunt. Igitur per 24^m huius, habent et reliqua latera singula singulis aequalia. Quare chordae kl mn invicem aequales erunt et chordae lm kn aequales et perinde arcus kl mn aequales, et reliqui⁴⁸ arcus lm kn invicem aequales erunt. 218 Verum arcus kl fuit duplum arcus ag et arcus mn duplum arcus cd, item arcus lm duplum arcus be atque arcus nk duplum arcus ah. 219 Ergo duplum arcus ag aequale duplo arcus cd et duplum arcus be aequale duplo arcus ah. Itaque et arcus, quorum dupla aequalia, aequales erunt, hoc est arcus ag aequalis arcui cd et arcus ah aequalis arcui be. 220 Item aio quod sinus anguli abc aequalis erit sinui arcus fg et vicissim sinus anguli agh aequalis erit sinui arcus fb. 221 Namque per hypothesim, sinus totus ad sinum arcus fg sicut sinus arcus bf ad sinum arcus fe. [S:51r] Per 6^m autem huius, sicut sinus arcus bf ad sinum arcus fe sic sinus totus ad sinum anguli abc. 222 Igitur sinus totus eandem rationem habet ad sinum anguli abc et ad sinum arcus fg et propterea aequalis erit sinus anguli abc sinui arcus fg. 223 Similiter cum per hypothesim sinus totus ad sinum arcus fb sit sicut sinus arcus gf ad sinum arcus fe. Et per 6^m huius, sinus arcus⁴⁹ gf ad sinum arcus fe sit sicut sinus totus ad sinum anguli agh. Iam et eandem rationem habebit sinus totus ad sinum anguli agh et ad sinum arcus fb; igitur aequalis erit sinus anguli agh sinui arcus fb. Et haec quidem proponebatur demonstranda.