[S:4]

THEOREMA IV

12 Potest signum plano tantum propinquare, ut planum ipsum fortius, verum particularius illuminet.

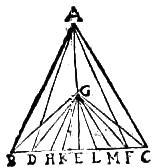
13 Signum A planum BC illuminet radiis AB, AD, AE, AF et AC, e quibus AE perpendicularis³⁹. Aio quod possibile est signum A tantum⁴⁰ propius fieri plano BC, ut magis per minorem ipsius plani partem illustret. Fiat enim propinquius signum A ipsi BC plano in signo G lineae AE, ita ut ductis radiis⁴¹ GB, GD, GE, GF et GC, angulus BGD minor fiat angulo BAD, hoc enim possibile est.⁴² Ducantur etiam GH ipsi AB, et GK ipsi AD, paralleli; item GL ipsi AF, et GM ipsi AC, paralleli radii. Ergo sub angulo BAC aequales sunt numero radii radiis sub angulo HGM comprehensis. Sed hi densiores.⁴³ Igitur per secundum suppositum erit planum HM illustratius plano BC. Radii vero sub angulo BAD plures sunt quam radii sub angulo BGD comprehensi; nam angulus ille est⁴⁴ maior[C:4v] hoc⁴⁵; per quintum ergo suppositum BD spatium magis illustratur⁴⁶ a radiis qui sub angulo BAD quam ab iis qui sub angulo BGD comprehenduntur. Idem de spatio FC demonstrabitur. Quare signum G plano BC propinquius quam signum A, ex toto BC, spatium dumtaxat HM vel fortasse ipsum DF illustrat⁴⁷, reliquum vero magis ab ipso A signo illustratur.