THEOREMA XI

29 Possibile est circuli ad planum obliqui umbram circularem proiici.

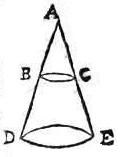
30 Esto enim ad hoc demonstrandum conus scalenus ABC, basim habens BC; qui quidem⁶⁴ plano per axim secetur ad rectos angulos basi, sitque communis sectio trianguli ABC. Secetur etiam plano ad ipsum ABC triangulum recto, sitque communis sectio conicae⁶⁵ superficiei et huius secantis plani conica sectio DE, communis vero sectio ipsius ABC trianguli et eiusdem plani recta DE, ponaturque ADE triangulum ipsi ABC⁶⁶ triangulo simile⁶⁷; eritque, ut in conicis demonstratur⁶⁸, co[C:6v]nica sectio DE circulus. Intelligatur ergo DE circulus a signo A illuminari⁶⁹, eritque umbra in planum, in quo circulus BC, proiecta, ipse circulus BC. Estque ipse DE circulus ad BC planum inclinatus. Igitur circulus ad planum, cui obliquus est, umbram proiicit circularem.