F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Diaphaneon, seu transparentium libellus Pars prima 1
<- App. -> <- = ->

PRIMA PARS LIBELLI11

Theorema I12

Quod13 per diaphanum planum transparet, maius quam sit, ac propinquius videtur, et14 eo maius15, quo propius plano diaphani.

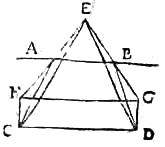
figura 1

4 Per diaphanum enim planum ab transpareat longitudo quaepiam cd per radios fractos eac et ebd et producantur in rectum radii ea et eb, donec cum ipsis cf, dg ad planum ab perpendicularibus [C:27v] concurrant in signis f, g et apparebunt signa c, d in signis f, g per ultimum suppositum. Longitudo ergo cd, quae absque diaphano16 sub angulo ced [S:32] appareret, nunc ad angulum feg maiorem17 spectatur. Et in terminis f, g. Quare maior et propinquior.

Inizio della pagina
 ->