74 Theorema XXIII

Si quod lumen, vel illuminatum quidpiam⁴⁶⁶ per sphaericum transpareat diaphanum, ad superficiem iuxta concursuum terminos appositam conversam sui formam proiiciet;⁴⁶⁷ aequalem sibi⁴⁶⁸ inquam⁴⁶⁹, dum tantum a sphaera distat, quantum et⁴⁷⁰ termini congressuum; dum autem magis⁴⁷¹, minorem; dum vero minus, maiorem.

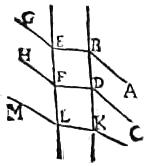
75 Per diaphanum globum ab transpareat lux quaedam, seu illuminatum quidpiam⁴⁷² cde ad oppositam superficiem fgh, in terminis congressuum positam, hoc est iuxta eum locum in quo ab unoquoque signorum⁴⁷³ rei cde progredientes per⁴⁷⁴ sphaeram radii concurrunt. Dico quod ipsius cde conversa imprimetur effigi[A:8r]es in ipsa fgh superficie. Procedant enim ab ipsis c, d, e⁴⁷⁵ signis radii cf, dg et⁴⁷⁶ eh, sese in sphaerae centro k secantes. 76 Et, quoniam fgh superficies est iuxta terminos, in quibus ab unoquoque ipsius cde rei signo per sphaeram transeuntes radii concurrunt, ideo ab ipso signo c per sphaeram ab transeuntes radii, cum cf qui per centrum, ad signum f omnes fere concurrent. Similiter, qui⁴⁷⁷ a signo d ad signum g quique⁴⁷⁸ a signo e ad signum h omnes⁴⁷⁹ fere cum ipsis dg et eh⁴⁸⁰ qui per centrum, congredientur. 77 Necnon a singulis⁴⁸¹ rei cde signis per sphaeram ab euntes radii ad singula⁴⁸² superficiei obiectae fgh [C:38r] convenient. Singulae igitur partes rei cde singulis superficiei fgh partibus suum impriment colorem distincte hoc est radio radium non impediente. Ergo ipsius rei cde ipsi superficiei fgh impressa spectabitur effigies. 78 Et, quoniam c in f, e vero⁴⁸³ in h radiat [S:48] ideo conversa. Et si dk⁴⁸⁴ fuerit⁴⁸⁵ aequalis ipsi kg, erit hf⁴⁸⁶ aequalis ipsi ce propter triangulorum aequalitatem. Ergo tunc effigies aequalis⁴⁸⁷ rei. Si autem dk maior⁴⁸⁸ quam kg, sequatur⁴⁸⁹, ut hf sit minor ce, effigies scilicet re⁴⁹⁰. Si vero minor, maior. Patet ergo theorema.

79 Corollarium

Patet ergo ratio, quare lux⁴⁹¹ vel aliquid⁴⁹² illuminatum per conspiciliorum vitrum transparens ad terminum quendam conversam porrigit⁴⁹³ effigiem, quandoquidem conspicilia superficiem habent utrinque convexam. 80 Immo in huiusmodi⁴⁹⁴ vitro talis conversa effigies expressior transparet⁴⁹⁵, quam⁴⁹⁶ si vitrum ipsum sphaericum esset. Et hoc, quia vitrum illud habet superficies, quae sunt parvae sphaerae portiones. Quare fit, ut parum absit, quin⁴⁹⁷ omnes ab uno signo radii ad⁴⁹⁸ unum congrediantur signum. Et ideo per singula puncta distincta imprimatur effigies.