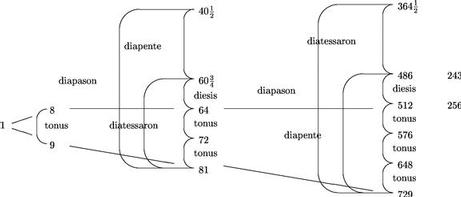
11 Praecedens autem hexachordum quod non infert tritonum, nec facit dictam tertii toni, in semitonia divisionem, nomen accepit a Natura quali medium inter duritiem et lenitatem5. 12 Electum autem fuit hexachordum quoniam6, ut alibi diximus, complectitur simplices omnes symphonias videlicet unisonum, tertiam, quartam, quintam, sextam, sive intervallis, unisonum, ditonum, diatessaron, diapente, ipsumque hexachordum. Quibus quidem intervallis singulis si adnectatur diapason, fient totidem [A:32r] symphoniae 2ae per compositionem. Nam diapason addita semper facit eiusdem qualitatis symphoniam. Itaque 13um spacium continebit 2i ordinis symphonias scilicet diapason .10mam.11am.12am.13am.
13 Adnectatur 13ae alia diapason. Et conflabitur 20a quae complet Icosichordum totum Guidonis quod complectitur 3ii ordinis systemata, scilicet disdiapason .17am.18am.19am.20am.
14
Itaque deinceps fieri potest in infinitum. Hinc patet origo numeri7 harum vocum hexachordum constituentium scilicet .ut . re . mi . fa . sol . la. Octo autem literae ![]() . a . b . c . d . e . f . g .8 statutae sunt ut earum unaquaeque octavo quoque loco repetita diapason consonantiam in proportione dupla semper indicet. Quod numeri in singulis chordis Icosichordi9 dispositi, sicut omnes alias consonantias et spacia ostendunt.
. a . b . c . d . e . f . g .8 statutae sunt ut earum unaquaeque octavo quoque loco repetita diapason consonantiam in proportione dupla semper indicet. Quod numeri in singulis chordis Icosichordi9 dispositi, sicut omnes alias consonantias et spacia ostendunt.
15 Continuatio autem tonorum in sesquioctava proportione, et constitutio, sesquialterae ac sesquitertiae proportionum. hoc est diatessaron ac diapente componentium diapason, ac dieseos spacium relinquentium sic patet in numeris.
16
.g. littera quare sonora dat initium hexachordo ![]() quadri et duri.
quadri et duri.
17 .c. quoniam media inter aspiratam et sonoram, dat initium hexachordo naturae diatonici generis.
18
.f. quoniam sapit ipsam10 aspiratam et mollem dat initium hexachordo ![]() mollis et chromatici generis.
mollis et chromatici generis.
[Fig. 4]
[A:32v]
19
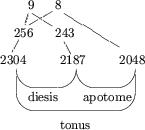
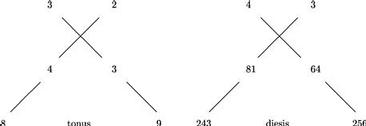
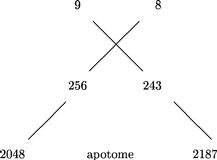
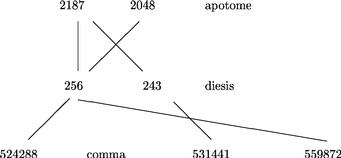
Ex quibus constat quod diesis proportio est in his numeris ... 256 ![]() 243. Videnda est nunc proportio semitonii maioris sive apotomes. Sic proportio 9
243. Videnda est nunc proportio semitonii maioris sive apotomes. Sic proportio 9 ![]() 8 facit tonum ducatur .9. in .256. et mox in .243. et fiunt duo numeri .2304. .2187. quorum proportio est sicut .256
8 facit tonum ducatur .9. in .256. et mox in .243. et fiunt duo numeri .2304. .2187. quorum proportio est sicut .256 ![]() 243, scilicet diesis. Item ducatur .256. in .8. et fiat .2048. Eritque sicut .9
243, scilicet diesis. Item ducatur .256. in .8. et fiat .2048. Eritque sicut .9 ![]() 8. sic .2304
8. sic .2304 ![]() 2048. Quare proportio .2304
2048. Quare proportio .2304 ![]() 2048. faciet tonum cumque proportio .2304
2048. faciet tonum cumque proportio .2304 ![]() 2187. faciat diesim, sive semitonium minus supererit proportio .2187
2187. faciat diesim, sive semitonium minus supererit proportio .2187 ![]() 2048. semitonii maioris scilicet apotomes.
2048. semitonii maioris scilicet apotomes.
[Fig. 5]
20 Calculus quantus extrahens apotomen differentiam toni et dieseos.
[Fig. 6]
[Fig. 7]
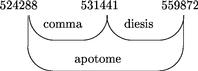
21 Differentia vero diesis et apotomes dicitur comma quod elicitur per subtractionem unius proportionis ab alia, ut infra patet.
[A:33r]
[Fig. 8]

[Marg. 1]
22 Constabit etiam quod diesis maior est, quam tria commata minor autem quam quatuor.
23 Apotome autem maior, quam .4or. commata, minor quam .5.
24 Unde et tonus excedet .8. commata et minor quam novem commata nascitur quae omnia ex longo et multarum figurarum calculo constari possunt11 lege Boetium et Fabrum in musicis elementis.
Octo chordarum distinctio per tonos et dieses.

[Tab. 5]
+ Die ![]() 30 december 156612
30 december 156612