11

44 Si sexanguli et decagoni in eodem circulo descriptorum latera componantur, composita tota extrema et media ratione secatur et maius segmentum est ipsius sexanguli latus.

Ut si in circulo abc descripti latus decagoni sit bc cui adnectatur in rectum be latus hexagoni in eodem circulo descripti, cuius diameter adc centrumque d. Aio, quod ce in puncto b extrema et media ratione secatur et maius segmentum be latus hexagoni.

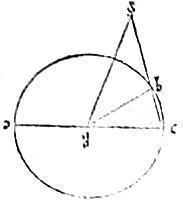
45 Erit enim angulus adb duplus ad angulum dbc per trigesimamsecundam Primi. Et angulus dbc duplus ad angulum e ergo angulus adb quadruplus ad angulum e. Sed idem angulus adb quadruplus ad angulum dbc per ultimam Sexti. Igitur anguli e et bdc aequales. Et idcirco triangula edc, cbd invicem aequiangula et similia. Quare sicut est ec ad ipsam cd hoc est ad ipsam eb sic erit cd vel eb ad ipsam bc. Atque ideo ec in puncto b extrema et media ratione secatur. Quod erat demonstrandum.

46 Quod si lineae extrema et media ratione divisae maius segmentum sit latus hexagoni in aliquo circulo descripti, tunc minus segmentum erit latus decagoni in tali circulo clausi. Item si minus segmentum ponatur latus decagoni, tunc maius erit latus hexagoni eiusdem circuli. Hae sunt quasi conversae huius undecimae. Et per ipsam undecimam et septimam huius demonstratur.