27.^a

72 Data circuli diametro, datur periferia.

Descripto enim circulo, super datam diametrum, datur periferia quamquam convoluta in ambitum. Sed quis vetat lineam convolutam explicare? Datur et in calculo, quam prope vis verum: quemadmodum irrationales lineae assignantur in numeris proprius ac proprius semper ad veritatem. 73 Quamvis ergo per Archimedem ostensum sit, rationem periferiae ad diametrum minorem quidem esse, quam triplam sesquiseptimam, maiorem vero quam triplam ac decem septuagesimas primas superpartientem: et a nobis [A:15r] etiam inter propinquiores limites conclusa sit; tamen in calculo semper contenti erimus proportione tripla sesquiseptima. Itaque datam diametrum multiplicabimus per 22 et productum in 7 partiemur: sic ex divisione, dabitur in quotiente periferiae quantitas.

28.^a

74 Data periferia circuli, datur diameter.

Ducta enim in septenarium data periferia: productoque in 22 diviso, dabitur quotiens, diametri scilicet magnitudo: quae duo data, per 7^am huius, absolvuntur.

29.^a

75 Dati circuli dabitur area.

Nam per quintam diffinitionem, circuli dati datur diameter: per antepraemissam, vero data diametro, datur periferia: dabitur ergo triangulum orthogonium, cuius laterum, quae circa rectum sunt angulum, alterum semidiametro circuli, alterum vero periferiae sit aequale, per 9^am huius: dabitur ergo, per 11^am huiusmodi trianguli area. 76 Sed talis area, ut demonstravit Archimedes, est aequalis areae circuli. Datur ergo area circuli. Producetur ergo area circuli ex ductu semidiametri in dimidium periferiae.

30.^a

Data circuli area, dabitur et diameter et periferia circuli.

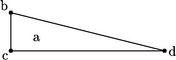
Esto enim area quaedam a data cuidam circulo aequalis. Dico quod dabitur talis circuli et diameter et periferia. 77 Erit enim aliquod triangulum orthogonium bcd, cuius angulus c rectus, et latus bc semidiametro, latus vero cd periferiae circuli³⁸ talis sit aequale. Quod quidem, per Archimedis demonstrata, erit areae circuli et perinde datae areae a aequale. Igitur ratio bc ad cd datur. Ergo per 23^am praemissi triangulum bcd datur specie. Datur autem magnitudine. Igitur per 35^am praemissi bc, cd semidiameter et periferia dantur.

[A:15v]

31.^a

78 Data sphaerae diametro; datur sphaerica superficies.

Nam, per 27^am huius, dabitur periferia circuli, cuius est talis diameter. Et per 29^am dabitur eiusdem circuli area. Sed ad talem aream sphaerica superficies est quadrupla, ut demonstrat Archimedes, dabitur ergo sphaerica superficies.

32.^a

Datae sphaerae dabitur soliditas.

79 Nam datae sphaerae datur diameter. Et per praecedentem, dabitur sphaerae superficies. Quae cum quadrupla sit ad circulum sphaerae maximum: et ad talem circulum quadruplus sit circulus duplam diametrum habens: iam hic circulus aequalis erit sphaericae superficiei. Sed conus hunc circulum basim habens et celsitudinem sphaerae semidiametro aequalem, iam aequiperat³⁹ soliditatem sphaerae; et datur idem conus: dabitur ergo sphaerae soliditas, ut demonstrat Archimedes.

33.^a

80 Data sphaerae superficie, datur eius diameter.

Nam si datur sphaerae superficies: datur et eius quarta pars. Sed haec quarta pars est area circuli in sphaera maximi per Archimedis demonstrata: datur ergo area circuli in sphaera maximi. Quare, per 30^am huius, datur huius circuli diameter: sed circuli maximi in sphaera diameter est ipsius sphaerae diameter. Datur igitur sphaerae diameter.

34.^a

81 Data sphaerae soliditate, datur eius diameter.

Sit data soliditas a sphaerae cuiusdam. Aio quod dabitur [A:16r] sphaerae talis diameter. Erit enim aliquis conus super basim b aequalem superficiei sphaericae et sub celsitudine bc aequali semidiametro sphaerae propositae. Qui conus per demonstrata Archimedis, aequalis⁴⁰ erit ad soliditatem sphaerae. 82 Dabitur igitur coni bc soliditas, quia scilicet aequalis⁴¹ soliditatis a datae. Scilicet coni talis diameter basis quadrupla est ad celsitudinem bc. Datur igitur conus bc specie ac magnitudine: dantur ergo eius dimetientes, per 26^am huius. Dabitur ergo bc sphaerae propositae semidiameter, ac perinde diameter.

Additio

Item circuli area data, dabitur diameter, sic.

83 Cum prope verum ratio circularis areae ad quadratum suae diametri sit sicut 11 ad 14, dabitur ergo diametri in tali circulo quadratum: ergo, per 3^am huius, dabitur talis quadrati latus quod est ipsius circuli diameter.

Similiter data sphaerae soliditate, dabitur diameter, sic.

Cum prope verum ratio soliditatis sphaericae ad cubum suae diametri sit sicut 11 ad 21, dabitur ergo talis cubus. Ergo, per 26^am huius, dabitur talis cubi latus, quod est ipsius sphaerae diameter.

Lineae

Diameter circuli --------- 7 Periferia ------------------ 22

Superficies

Area circuli --------------- 11 Quadratum diametri 14 Superficies sphaerae ------ 44

Solida

Soliditas sphaerae ------------ 11 Cubus diametri sphaerae 21 Conus ------------------------------ 2 3/442 Cylindrus ------------------------ 8 1/443

In arce Catanensi, 13 aprilis 1554