[A:22v] ELEMENTORUM OCTAVUS

p^a

1 Maximus numerus numerans duos numeros: numerat eos secundum quotientes minimos illis proportionales.

Patet, quoniam maior divisor facit minores ex divisione quotientes et maximus minimos, ac divisis proportionales. 2 Per quintam praemissi quoniam scilicet ex divisorem in quotientes per multiplicato producuntur divisi.

Corollarium

Hinc manifestum est quod primi ad invicem numeri (quoniam a sola unitate numerantur secundum ipsosmet) sunt proportionalium minimi.

3 Contra proportionalium minimi sunt inter se primi: nam, si compositi, haberent communem mensuram secundum quotientes minores, quod esset supposito contrarium.

Corollarium

4 Item hinc sequitur, ut minimi numeri in aliqua ratione semper numerent numeros sibi proportionales secundum maximam eorum mensuram.

Singuli secundum singulos¹.

Corollarium

5 Utique maxima mensura duorum numerorum dividens eos singulos exhibeat quotientes in tali ratione minimos.

2^a

Si duorum numerorum inter se primorum alterum metiatur tertius tunc hic ad reliquum illorum erit primus.

6 Sint a, b numeri primi ad invicem quorum unum a metiatur tertius² c tunc b, c primi erunt inter se. Nam si quispiam metiretur eos, idem numeraret ipsum a et essent a, b compositi quod est contra hypothesim.

3^a

7 Duorum numerorum primorum ad tertium, productus ad eundem primus est.

Numeri a, b primi sint ad c. Ipsorum autem a, b productum sit d. Tunc c, d primi ad invicem erunt. Secus enim, metietur eos quispiam, qui sit e. 8 // Et quoniam c, a primi ad invicem, ipsum autem c metitur ipse e. Ideo, per praecedentem, [A:23r] a, e primi sunt ad invicem. Quoties autem e ipsum d metitur, tot unitates sunt in f unde tunc ex f in e fiet d. 9 Sed ex a in b fit d. Igitur, per 3^um corollarium 6^ae praemissi, erit sicut e  a sic b  f. Sed e, a primi ad invicem. Ergo, per p^um corollarium primae huius, minimi sunt in tali ratione³: et per sequens corollarium e metitur ipsum b metiebatur autem et ipsum c. Ergo b, c compositi ad invicem: quod est contra hypothesim. Igitur c, d primi sicut proponitur.

Corollarium

10 Hinc sequitur, ut numeri cuiuslibet primi ad aliquem, tam quadratus, quam cubus, quam secundus quadratus et sequentes in proportione⁴ continua, sint ad eundem primi.

Corollarium

11 Utque si duorum uterque ad aliorum duorum utrumque primus sit: et illorum productus horum producto primus sit.

Corollarium

Item ut, cum duo numeri ad invicem primi genuerint in suos singuli ordine quadratos, cubos, secundos quadratos, et successive reliquos in proportione continua: tunc singuli unius ordinis numeri ad singulos quoslibet alterius ordinis collati erunt ad invicem primi.

4^a

12 Numerus primus non metiens alterum est ad ipsum primus.

Numerus a primus⁵ non metiatur ipsum b. Dico quod a, b primi sunt ad invicem. Nam si quispiam, ut c metiatur ipsos, non erit idem cum a. Et ideo ipsum a primum metietur alius quam ipsemet. Quod est impossibile.

5^a

13 Primus metiens productum metitur alterum multiplicantium. Saltem.

Ex a in b fiat c quem d primus metiatur. Tunc d saltem ipsorum a, b alterum metietur. Sit enim ut d ipsum a non metiatur: eruntque per praemissam ipsi a, d [A:23v] ad invicem primi c, a primus sit d. // Quoties autem d ipsum c metitur, tot unitates sint in e. Ita hinc cum ex d, e fiat c et ex a, b fiat idem c, iam per 3^um corollarium 6^ae praemissi libet erit sicut d  a sic b  e. 14 Sed d, a primi ad invicem ergo, per p^um corollarium primae huius, minimi sunt in tali ratione: quare, per sequens coroll d, a metientur ipsos a, b singuli singulos secundum ordinem proportionis. Itaque d metietur ipsum b omnino ergo saltem unum ipsorum a, b metitur.

6^a

15 Compositum numerum aliquis primus metitur.

Nam si qui metitur compositum, sit primus; constat propositum. Secus metiatur metientem aliquis, donec veniatur ad primum. Omnis enim numerus numerans numerantem numerat numeratum.

7^a

16 Propositus duobus numeris, invenire minimum, quem metiuntur.

Sint duo numeri a, b oportet invenire minimum ab eis numeratum. Si a, b primi sunt ad invicem tunc ex a in b fiat c: erit enim c minimus numeratus ab ipsis a, b quoniam scilicet multiplicantes numerant productum. 17 Si autem numerus minor, quam c sit⁶ quem numerent ipso a, b sit ille d quem ipso a, b metiantur per ipsos e, f quotientes. Ita hinc a, f ipsum b multiplicantes efficiunt ipsos c, d. Et ideo per 5^am praecedentis, sicut a  f sic c  d. Sed c maior, quam d. 18 Ergo et a maior, quam f. Similiter ostendam quod b maior, quam e⁷. Cumque ex a in e fiat d⁸. Et ex b in f fiat d; iam per 3^um corollarium 6^ae praemissi, sicut a  b sic f  e. Sed a, b primi ad invicem, per corollarium p^um primae huius, sunt minimi suorum proportionalium. Nunc autem maiores ipsis f, e proportionalibus. Quod est impossibile. Non est igitur numerus minor, quam c quem ipsi a, b metiantur.

// 19 Quod si numeri a, b propositi sint invicem compositi. Tunc non erunt minimi suorum proportionalium, per corollarium primum p^ae huius. Inveniantur ergo minimi, per 3^um corollarium p^ae huius, qui sint c, d. Ita [A:24r] tunc, per 3^um corollarium 6^ae praemissi, qui ex b in c erit is, qui ex a in d qui quidem sit e nam hic erit minimus, quem a, b metiuntur. 20 Nam tunc ipsi a, b metiuntur ipsum e secundum ipsos c, d quotientes. Si autem numerus minor, quam e sit, quem metiuntur ipsi a, b sit ipse f quem ipsi a, b metiantur secundum ipsos g, h quotientes. Ita tunc ex a in g fit f. Et ex b in h fit f. Quare per 3^um corollarium 6^ae praemissi, est sicut h  g sic a  b et ideo sicut c  d. 21 Et quoniam c, h multiplicantes ipsum b faciunt ipsos e, f, ideo per 5^am praemissi, erit sicut c  h sic e  f. Sed e maior, quam f ergo c maior, quam h. Et similiter ostendetur d maior, quam g. Quare ipsi hg sunt minores ipsis c, d⁹ sibi proportionalibus: igitur c, d non sunt minimi proportionalium, sicut proponebantur. Et idcirco non erit numerus minor, quam e quem ipsi a, b metiantur.

Aliter

22 Quando a, b sunt primi ad invicem tunc dico, quod c productus ab eis est minimus, quem metiuntur. Ponatur enim alius, quem ipsi a, b metiuntur, qui sit d secundum quotientes e, f. // Eritque sicut a  b sic f  e. Et sicut a  f sic c  d. Cumque a, b sint minimi suorum proportionalium, iam per corollarium 2^um primae huius, a metietur ipsum f. 23 Et ideo c metietur ipsum d. Quare c minor quam d. Et similiter ostendetur minor omni alio, quem metiuntur ipsi a, b.

a   b 3   5   c   15   d   30 e   f 10   6

a  b sicut f  e quoniam

ae  bf

d

a  f sicut c  d quoniam b

a  c f  d

24 Quando vero a, b sunt compositi, inveniantur, ut prius, primi ad invicem, et in tali ratione minimi, qui sint c, d. Et ex a, d vel ex b, c producatur, ut antea, e. Qui, nunc erit minimus, quem ipsi a, b metiuntur. Ponatur enim alius, quem metiantur ipsi a, b qui sit f secundum [A:24v] quotientes g, h. 25 // Eritque ut ante, sicut h  g sic a  b et ideo sicut c  d. Item sicut c  h sic e  f. Cumque c, d sunt minimi huius rationis, iam per 2^um corollarium primae huius c metietur ipsum h et ideo e metietur ipsum f. Quare e minor, quam d. Et similiter ostendetur minor omni alio, quem metiuntur ipsi a, b.

a b c d e f g h 12 20 3 5 60 120 10 6

h  g sicut a  b <sicut> c  d quoniam

ag  bh

f

c  h sicut e  f quoniam b

c  e h  f

Corollarium

26 Ex qua demonstratione manifestum est quod minimus numerus, quem duo numeri metiuntur, metitur omnem alium ab eisdem duobus numeratum.

8^a

27 Propositis tribus numeris,maximum eos numerantem invenire.

Sunto tres numeri a, b, c. Inveniatur per 4^am praecedentis, maxima ipsorum a, b mensura, qui sit numerus d, qui si metitur ipsum c, erit iam maxima trium a, b, c dimensio. Secus sit e maxima ipsorum cd mensura nam ipse erit maxima ipsorum a, b, c dimensio. Aliter enim maior metiretur minorem, ex corollario 4^ae praedictae.

a b c d e 36 24 15 12 3

9^a

28 Propositis quoque tribus numeris,invenire minimum, quem metiuntur.

Sunto tres numeri a, b, c. Sit antepraemissam d minimus numeratus ab ipsis a, b. Et si c numerat ipsum d¹⁰ absolutum est problema. Sin vero, sit e minimus numeratus ab ipsis d, e. Nam tunc ipse e erit minimus, quem metiuntur tres ipsi a, b, c. [A:25r] Aliter enim, per corollarium antepraemissae, sequitur ut maior metiatur minorem¹¹.

a b c d e 12 9 5 36 180

10^a

29 Si extremi quotcumque numerorum continue proportionalium fuerint primi ad invicem: tunc tales numeri minimi sunt omnium sibi proportionalium.

Nam si extremi primi, ergo, per corollarium primae huius, omnium expositorum in eadem ratione et numero extremos singuli singulos, metientur: et ideo medii medios, singillatim. 30 Atque ideo minores quibuslibet expositis sibi proportionalibus erunt singuli singulis. et perinde suorum proportionalium minimi.

11^a

Datam rationem in minimis numeris, continuare bis, ter, quater, et quotiescumque in minimis etiam numeris.

31 Sit data ratio in minimis numeris 2, 3 multiplicet 2 se ipsum, et faciat 4 multiplicet 3 et faciat 6, multiplicet 3 se ipsum, et faciat 9. Item 2 multiplicet 4 et 6 et faciat 8 et 12. At 3 multiplicans 6 et seipsum faciat 18 et 27. Adhuc¹² 2 multiplicans 8, 12, 18, 27 faciat 16, 24, 36, 54. Et 3 multiplicans 27 faciat 81. 32 Quamque et 3 multiplicans 12 et 18 fecisset item 36 et 54 propter proportionem multiplicantium et multiplicatorum. Undes ergo sub unitate quadruplicem ordinem numerorum.

Primum 2, 3 minimorum in ratione data. Secundum 4, 6, 9 ubi duplicatur data ratio. 33 Tertium 8, 12, 18, 27 ubi ratio triplicatur. Quartum 16, 24, 36, 54, 81 ubi ratio eadem quadruplicatur in¹³ proportione continuata. [A:25v] Quod enim numeri sint proportionales constat per 5^am praemissi.

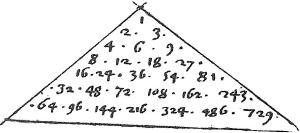
Quod vero numeri in singulis ordinibus sint invicem primi patet per corollarium 3^um tertiae huius, et per praecedentem. 34 Quin etiam si 2, 3 similiter multiplicent singulos numeros quarti ordinis ratio producto, gignentur numeri sex quinti ordinum 32, 48, 72, 108, 162, 243 quinquies continuates eandem datam rationem. Demum, si lubet, ipsi 2, 3 multiplicent adhuc dictos numeros quinti ordinis: et fient septem numeri in sexto ordine, sexcuplicantes eandem rationem continue. 35 Atque ita in infinitum. // In minimis numeris repetita dicti corollarii, ac praecedentis argumentatione.

Considera in hac descriptione quadruplicem seriem numerorum, scilicet transversorum¹⁴ unitatem et sex ordines productos, in quibus singulis, semel, bis, ter, quater, quinquies et sexies, continuatur ratio sesquialtera.

36 Secunda est series obliquorum ad sinistram, continens sex ordines aequidistantes, primum 1, 2, 4, 8, 16, 32, 64 et quinque sibi parallelos. In quibus singulis toties continuatur dupla ratio.

37 Tertia est series obliquorum ad dextram¹⁵, continens totidem ordines, primum 1, 3, 9, 27, 81, 243, 729 et quinque sibi aequidistantes, in quibus singulis toties continuatur¹⁶ ratio tripla. Ut constat per 9^am praecedentis.

38 Quarta series est descendentium perpendiculariter continens novem ordines, medium 1, 6, 36, 216 ad eius sinistram quatuor, et totidem ad dextram, in quibus singulis continuatur ratio sexcupla: quippe¹⁷ quae per medium terminum ubique componitur ex tripla et dupla. [A:26r]

39 Quae, quidem consideratio, sicut in hac descriptione fit per ratione sesquialtera, quae sub terminis 2, 3 minimis continentur, ita fieri potest per quacumque alia ratione, sub suis numeris minimis assignata. Atque per eandem demonstrationem, propositus est ultus¹⁸ ad omnem datam sub suis infimis terminis rationem. Ex qua consideratione sequuntur multae propositiones.

12^a

40 In numeris continue proportionalibus, si primus non metitur secundum, nullus eorum metieur alium.

Patet in ordinibus dictae descriptionis transversis.

13^a

41 Quod si primus¹⁹ metitur secundum, metietur omnem alium in sequentibus. Contra si primus metiatur postremum, metietur secundum.

Haec 13^a patet in ordinibus obliquis ad levam et dextram et eorum aequidistantibus. Item in descendentibus. Eius conversa patet per praecedentem a destructione contrarii.

14^a

42 Si primus non metitur postremum, non metietur secundum.

Patet per 12^am a destructione contrarii.

15^a

Quot medii proportionales interiacent duobus numeris primis; totidem inter utrumque ipsorum et unitatem cadunt. Et e contrario.

Constat utrumque, si conferas ordinem transversum, cum obliquo.

16^a

43 Duorum quadratorum unus. Cuborum duo. Quadratorum secundorum tres medii proportionales existant.

Patet hoc in ordinibus numerorum ordinibus.

17^a

Numerorum continue proportionalium, tam quadrati quam cubi, quamque secundi quadrati, nec non et quadrati cubici, sunt etiam continue proportionales.

44 Patet in transversis et obliquis ordinibus. Quoniam in quadratis ratio lateri²⁰ duplicatur. In cubis triplicatur. In quadratis cubicis sexcuplicat. Quod in dictis ordinibus similiter manifestum est.

18^a

45 Si latus metitur latus, et quadratus quadratum metietur et e contrario. Item si latus a latere mensuratur: et cubus a cubo mensurabitur et e converso.

Si vero latus a latere non numeretur, nec quadratis a quadrato numerabitur et e contrario. Item si, latus a latere non numeretur: nec cubus a cubo numerabitur et e contrario. Idem conclude de planis similibus et²¹ solidis similibus. [A:26v] Constat haec, sicut 12^a, 13^a et 14^a huius.

19^a

46 Duobus planis similibus unus. Duobus autem solidis similibus duo medii proportionales interiacent.

Patet in ordinibus obliquis quoniam ipsorum 6, 12, 24 extremi sunt similes plani et alii infiniti. Item ipsorum 3, 6, 12, 24 extremi sunt similes solidi, et alii.

2 6 4 24 3 6 Similes plani

1 1 1/2 3 2 6 24 1 1/2 3 2 4 Similes solidi

20^a

47 Duo numeri, quorum unus est medius proportionalis, similes plani sunt. Quorum vero duo sunt medii proportionales similes solidi sunt.

Quoniam scilicet illi sunt proportionales quadratis his vero cubis. Et in illis semper ratio respondentium laterum est subdupla, in his vero subtripla rationis ipsorum.

21^a

48 Si trium numerorum continue proportionalium primus fuerit quadratus et postremus quadratus erit. Si vero quatuor continue proportionalium primus fuerit cubus: Et quartus cubus erit. Item, si quinque numerorum continue proportionalium primus sit quadratus secundus: et quintus erit quadratus secundus erit. 49 Adhuc si septem numerorum continue proportionalium primus sit quadratus cubicus. et septimus quadratus cubicus erit.

Patet in ordinibus tam transversis, quam obliquis et quoniam in descendentibus simul sint proportionales²².

22^a

50 Quadrati sunt proportionales quadratis; cubi, cubis. Et e contrario²³ Item similes plani sunt proportionales quadratis. Et similes solidi proportionales cubis.

Patet, quoniam ibi duplicatur, hic triplicatur proportio laterum eadem. 51 Contra numeri proportionales quadratis, inter se similes plani. proportionales vero cubis, similes solidi sunt. Quoniam, scilicet illi habent unum medium proportionalem sicut quadrati. Hi autem duos, sicut cubi et ideo per antepraemissam constat propositum. Item proportionalium radicem secunda quadrata sunt proportionalia. Et e contrario.

17 februarii