|
Propositio 89a
398
Omnis impar in quadratum secundae speciei, hoc est centralem, sibi collateralem multiplicatus, producit gnomonem collateralem ex ordine gnomonum ab unitate continuatorum, atque quadratos ex quadratis primis in se ductis genitos per additionem [S:55] successivam constituentium.
399
Praemissa unitate, quae omnem numeri speciem repraesentat, secundus impar est 3, secundus autem quadratus centralis est 5, ex horum ducto fit 15 gnomo secundus quippe qui cum unitate facit 16 quadratum scilicet quaternarii. Quod sic ostendo: post unitatem [C:58v] notabo primum duos, inde428 tres, inde429 quatuor, inde430 quinque numeros ab unitate per duplam proportionem notatos.
400
Hoc pacto duo primi numeri scilicet 1, 2 per sextam huius simul conficiunt imparem secundi loci, scilicet 3. Extremi autem sequentis ordinis scilicet 1, 2, 4 sunt 1 et 4 proximi scilicet quadrati, quorum congeries, per sexagesimam octavam huius est quadratus centralis secundi loci, scilicet 5.
401
Itaque demonstrandum est quod aggregatum ex uno et 2 multiplicatum in congeriem ex 1 et 4 producit gnomonem secundi loci, hoc est differentiam ipsorum 1 et 16 qui sunt quadrati quadratorum, primus unitatis, et alter quaternarii. Talis enim gnomo, scilicet 15, appositus unitati, constituit 16 quadratum quadrati secundi431.
402
Nam in hisce quatuor numerorum ordinibus, duo primi, scilicet 1, 2 sunt432 differentiae trium sequentium, scilicet 1, 2, 4 et rursus hi tres sunt differentiae quatuor sequentium, scilicet 1, 2, 4, et 8 et adhuc hi quatuor sunt differentiae quinque postremorum, scilicet 1, 2, 4, 8, 16 quandoquidem in numeris continue proportionalibus differentiae sunt continue proportionales, et primae differentiae sint iam unitates, sicut primi ordinum singulorum numeri.
403
Hic est autem processus demonstrationis: aggregatum ex uno et 2 primi ordinis ductum in unitatem, facit congeriem 1 et 2 in tertio ordine. Item aggregatum ex 1 et 2 primi ordinis [C:59r] ductum in 4 producit 4 et 8 in tertio ordine, hoc est433 12.
404
Igitur tale aggregatum ex 1 et 2 hoc est 3 ductum in congeriem ex 1 et 4 hoc est in 5, producet cumulum quatuor numerorum, scilicet 1, 2, 4, 8. Verum talis cumulus facit cumulum differentiarum quarti ordinis, scilicet ipsorum 1, 2, 4, 8, 16 et proinde434 facit differentiam extremorum, scilicet 1 et 16, hoc est 15 gnomonem secundi loci praedictum. Quod fuit demonstrandum.
405
Item dico quod tertius impar, scilicet 5, ductus in tertium quadratum centralem, scilicet 13, producet tertium gnomonem ex praedictis, scilicet 65 qui scilicet cum 16 coniunctus facit quadratum novenarii, qui tertius quadratus est, facit inquam 81 quadratum ex quadrato tertio in se ducto435 genitum. Quod haud obscure, nec difficilius ostendam, hoc processu. [S:56]
406
Post unitatem notabo radices proximas secundi et tertii loci, scilicet 2 et 3 qui, per sextam huius coniuncti faciunt tertium imparem; mox duco 2 in se et in 3, nec non 3 in se et fient 4, 6, 9 continue proportionales in ratione ipsorum 2 et 3; et rursum436, ex quatuor multiplicationibus, scilicet ex ductu 2 in 4 et in 6 et ex ductu 3 in 6 et in 9, fiant437 quatuor numeri similiter proportionales 8, [C:59v] 12, 18, 27.
407
Et adhuc ex quinque multiplicationibus, scilicet ex 2 in singulos dictos438 quatuor439 8, 12, 18, 27 et ex 3 in 27 fiant quinque numeri 16, 24, 36, 54, 81 in eadem ratione continua proportionales. Atque his constitutis, demonstrandum erit quod aggregatum ex 2 et 3 scilicet 5 tertius impar, multiplicatum in aggregatum ex 4 et 9, hoc est in 13, quod, per sexagesimam octavam, est tertius quadratus centralis, producit differentiam ipsorum 16 et 81, hoc est, gnomonem ex his, quales diximus tertium.
408
Nam per vigesimam primam septimi Elementorum Euclidis, quoniam ex ductu ipsorum 2, 3 primi ordinis nascuntur numeri trium reliquorum ordinum, idcirco singuli ordines servant continuam proportionem primi; et quoniam440 ex multiplicante in differentiam441 multiplicatorum, producitur differentia productorum, idcirco, duo numeri primi ordinis, scilicet 2 et 3, sunt differentiae numerorum sequentis ordinis, scilicet ipsorum 4, 6 et 9; et similiter hi tres sunt differentiae numerorum quarti ordinis, qui sequitur, scilicet ipsorum 8, 12, 18, 27.
409
Nec secus hi quatuor442 sunt differentiae quinque numerorum sequentium, scilicet 16, 24, 36, 54, 81; quo fit, ut cumulus ipsorum 8, 12, 18, 27 sit differentia ipsorum 16, 81 extremorum. [C:60r] Unde demonstrandum erit, quod ex multiplicatione aggregati ipsorum 2, 3 in congeriem ipsorum 4 et 9 hoc est ex ductu 5 in 13, tertii scilicet imparis in tertium quadratum centralem, producitur cumulus ipsorum 8, 12, 18, 27, hoc modo.
410
Quoniam ex 2 in 4 fit 8 et ex 3 in 4 fit 12 per vigesimam tertiam septimi Euclidis (quoniam 2 ad 3 sicut 8 ad 12443) propterea ex 4 in aggregatum ipsorum 2, 3 fit aggregatum ipsorum444 8, 12 per primam secundi Elementorum, et per eandem rationem, quoniam ex 2 in 9 fit 18 et ex 3 in 9 fit 27, propterea ex 9 in aggregatum ipsorum 2, 3 fit aggregatum ipsorum 18, 27.
411
Rursum ergo ex prima secundi Euclidis, sequitur445 ut ex aggregato ipsorum 2, 3 in aggregatum ipsorum 4, 9 fiat cumulus quatuor numerorum 8, 12, 18, 27. Quod fuit demonstrandum. [S:57] Eodem penitus processu demonstrabimus quod quartus impar scilicet446 7447 ductus in quadratum centralem quartum 25 efficit 175 gnomonem quartum, qui cum quadrato novenarii iunctus, scilicet cum 81, componit quadratum ex 16, scilicet 256.
412
Item similiter ostendemus quod quintus impar, scilicet 448 9, ductus in quintum quadratum centralem, scilicet 41, producit 369, gnomonem quintum qui cum 256 constituit 625 qui quadratus est quinti quadrati; et sic in infinitum. |
|
|
Pro secundo loco. |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
2 |
|
|
|
1 |
|
2 |
|
4 |
|
|
1 |
|
2 |
|
4 |
|
8 |
|
1 |
|
2 |
|
4 |
|
8 |
|
16 |
|
|
|
|
|
3 |
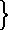 |
15 |
|
5 |
|
|
|
|
|
Pro tertio loco. |
|
|
|
|
|
1 |
|
|
|
|
2 |
|
3 |
|
|
|
4 |
|
6 |
|
9 |
|
|
8 |
|
12 |
|
18 |
|
27 |
|
16 |
|
24 |
|
36 |
|
54 |
|
31 |
|
|
|
|
|
5 |
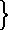 |
65 |
|
13 |
|
|
|
|
|
Pro quarto loco. |
|
|
|
|
|
1 |
|
|
|
|
3 |
|
4 |
|
|
|
9 |
|
12 |
|
16 |
|
|
27 |
|
36 |
|
48 |
|
64 |
|
81 |
|
108 |
|
144 |
|
192 |
|
256 |
|
|
|
|
|
7 |
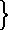 |
175 |
|
25 |
|
|
|
|
|
Pro quinto loco. |
|
|
|
|
|
1 |
|
|
|
|
4 |
|
5 |
|
|
|
16 |
|
20 |
|
25 |
|
|
64 |
|
80 |
|
100 |
|
125 |
|
256 |
|
320 |
|
400 |
|
500 |
|
625 |
|
|
|
|
|
9 |
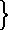 |
369 |
|
41 |
|
|
[C:60v]
|
|
|
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
Impares |
|
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
Quadrati primi |
|
1 |
5 |
13 |
25 |
41 |
61 |
85 |
113 |
145 |
181 |
Quadrati centrales |
|
1 |
15 |
65 |
175 |
369 |
671 |
1105 |
1695 |
2465 |
3439 |
Gnomones |
|
|
|